
В одному з попередніх уроків ти дізнався про властивості предметів і як вони пов'язані з математикою. На цьому уроці ти познайомишся з поняттям - математична закономірність.
Закономірності, як і властивості предметів пов'язані з математикою і з логікою. Знаючи закономірність, ти точно можеш знати, що буде далі. Після четверга точно буде п'ятниця, після 10 години ранку буде 11 година ранку. Послідовність дій, явищ, властивостей або подій в закономірності завжди визначена, тобто ми точно знаємо що буде далі.
Типи закономірностей
Існує кілька типів закономірностей: убуваючі, зростаючі, циклічні і складні закономірності. Давайте познайомимося з кожної докладніше
Зростаюча закономірність
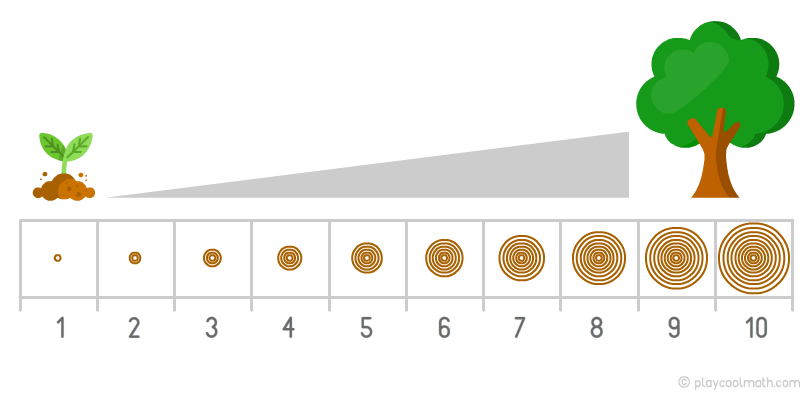
Наприклад, дерево росте і на його стовбурі щороку додається одне нове кільце. Цей процес називається простою зростаючою закономірністю. У цій закономірності легко обчислити, скільки кілець буде через 2 роки або через 10 років. Кількість кілець в стовбурі відповідає віку дерева.
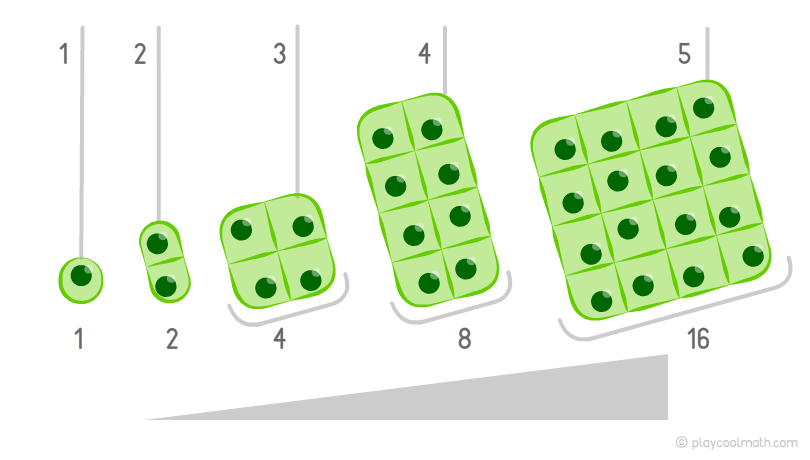
Наведемо приклад зростаючої закономірності, яка складніше ніж в прикладі з деревом. Уявіть одноклітинний організм, який щохвилини ділиться на дві клітини. На зображенні добре видно, що в першу хвилину ми бачимо 1 клітку, в другу - вже 2 клітини, а потім 4 клітини, 8, 16. Кожну хвилину кількість збільшується в 2 рази. Знаючи попередню кількість, можна дізнатися, скільки буде клітин в наступну хвилину. Цей процес називається теж зростаючої закономірністю. Для справжніх математиків буде нескладно встановити формулу збільшення закономірності для цього прикладу. Це завдання для тебе ще складне, так як ти тільки почал вивчати математику. Головне зараз щоб ти зрозумів, що таке закономірність.
Убуваюча закономірність
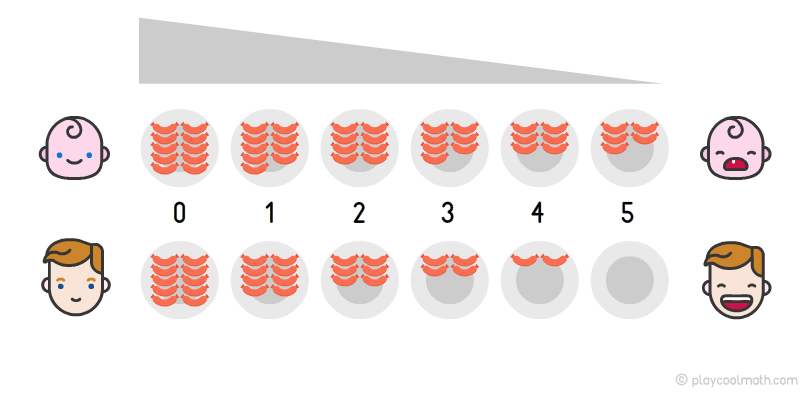
Уявіть змагання з поїдання сосисок на швидкість, в яких беруть участь два учасники. У кожного по 10 сосисок на тарілці (це стільки, скільки у тебе пальців на руках). Перший з'їдає одну сосиску за хвилину, а другий з'їдає 2 сосиски за хвилину. Ясно, що другий учасник змагань переможе, так як він з'їдає більше сосисок за хвилину, ніж перший учасник. Але нам важливо побачити закономірність. На малюнку ми можемо побачити, як в кожній тарілці зменшується кількість сосисок. Цей процес називається спадною або убуваючою закономірністю. Другий учасник з'їв всю тарілку сосисок за п'ять хвилин і переміг!
Циклічна закономірність
Ти точно знаєш закономірність такого типу - це зміна пір року. Весна-Літо-Осінь-Зима і потім відбувається повторення.
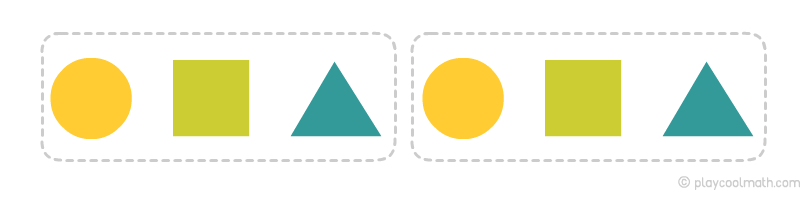
Розглянемо приклад з предметами різної форми. На малюнку ти бачиш ланцюжок з різної кількості предметів. Спробуй знайти закономірність на малюнку нижче. Продовжи ланцюжок.

Предмети повторюються через кожні три осередки. Знаючи закономірність, ми можемо припустити, які предмети будуть далі. За останньою ланкою буде трикутник, потім коло, далі квадрат.
Складні закономірності
Розглянемо приклад закономірностей на одному і тому же ланцюжку, але будемо шукати закономірності в залежності від властивості ланок. Спробуй знайти наступна ланка в прикладі нижче.

Закономірність за формою
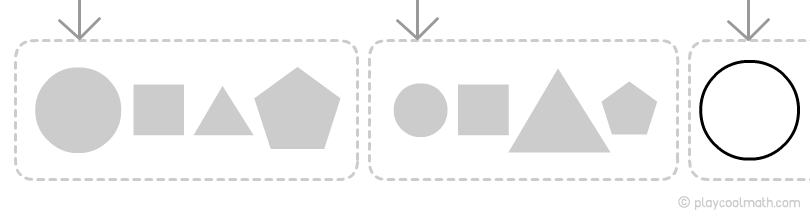
Бачимо, як чергуються ланки ланцюжка. Точно знаємо, що за формою наступним буде коло, позначимо його як велике коло
Закономірність за розміром
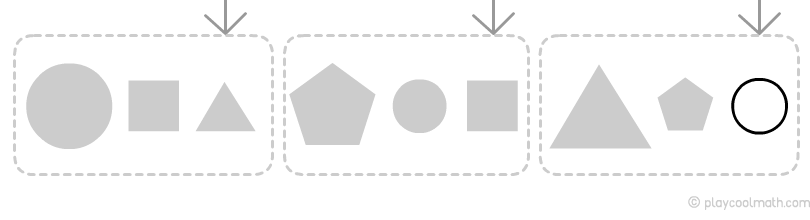
Бачимо, як чергуються ланки ланцюжка: велика і потім дві маленькі фігури, тобто наступною буде маленька фігура.
Закономірність за кольором
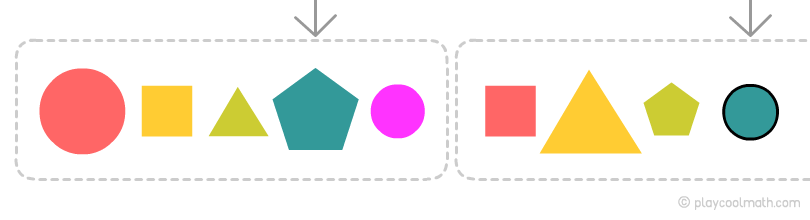
Вийшла найдовша закономірність в ланцюжку, виділимо її і визначимо, який буде наступний колір.
Як бачиш, закономірність залежить від властивостей елементів ланцюжка. Для одного і того ж ланцюжка ми знайшли різні закономірності в залежності від властивості. Об'єднаємо отримані результати і дізнаємося, яка ланка будуть наступною.

Алгоритм пошуку закономірностей
Давайте ще раз повторимо всі кроки для виявлення закономірностей.
- Визначаємо кількість властивостей ланцюжка;
- Визначаємо закономірність для кожної властивості;
- Порівнюємо закономірності для визначення всіх властивостей наступної ланки в ланцюжку.
Пошук закономірностей - це дуже гарний навик для юного математика. У майбутньому, коли ти будеш вивчати цифри, тобі обов'язково ця навичка знадобиться. Ми створили набір тестів, де ти зможеш потренуватися в пошуку закономірностей. Спробуй пройти всі тести з хорошим результатом і рухайся далі у вивченні математики.


