
In one of the previous lessons, you learnt about the properties of objects and how they are related to maths. In this lesson, you will learn the concept called a mathematical pattern.
Patterns like object properties are related to maths and logic. Knowing the pattern, you can know exactly what will happen next. Friday will come after Thursday, 11 o'clock comes after 10 o’clock in the morning. The sequence of actions, phenomena, properties or events in the patterns is always defined. That is why, we know exactly what will happen next.
Types of patter
There are several types of patterns: decreasing, increasing, cyclic and complex patterns. Let's learn with each of them in details.
Increasing pattern
For example, a tree grows and one new ring is added to its trunk every year. This process is called a simple increasing regularity. In this pattern, it is easy to calculate how many rings will appear in 2 years or in 10 years. The number of rings in the trunk corresponds to the age of the tree.
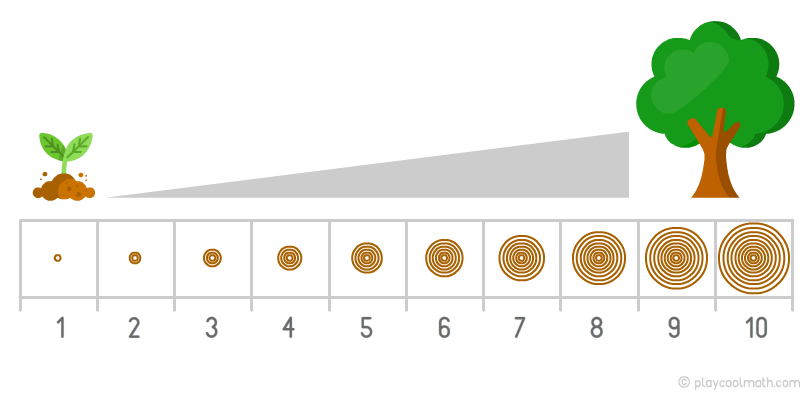
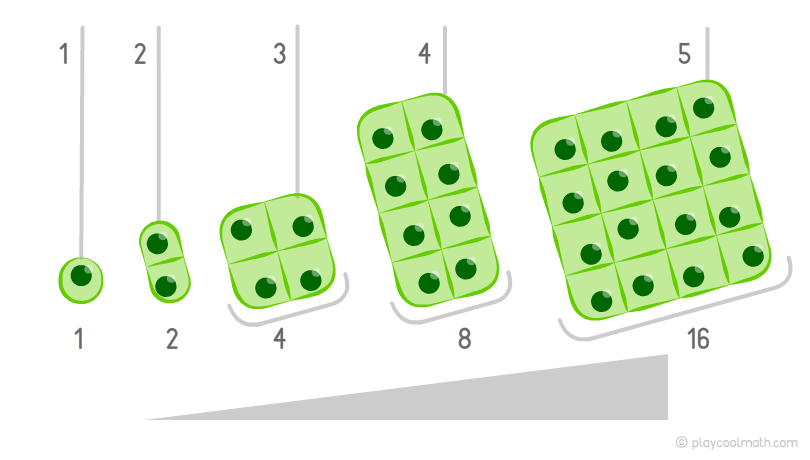
Let's give an example of an increasing pattern that is more complicated than the one in the example with a tree. Imagine a single-celled organism that is divided into two cells every minute. The picture clearly shows that during the first minute we see 1 cell, during the second minute - already 2 cells, and then 4 cells, 8, 16. Every minute the amount increases twice. If you know the previous number, you can find out how many cells will appear within the next minute. This process is also called an increasing pattern. For true mathematicians, it will not be difficult to find out a formula for increasing the pattern for this example. This task is still difficult for you, since you have just started to study maths. The main thing is to understand what a pattern means.
Decreasing pattern
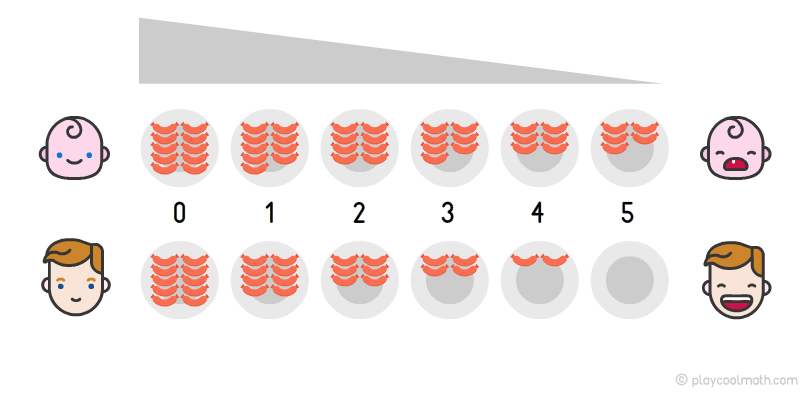
Imagine a competition of eating sausages at a speed where there are two participants. Everyone has 10 sausages on a plate (it is as much as your fingers). The first one eats one sausage per minute, and the second one eats 2 sausages per minute. It is clear that the second participant will win as he eats more sausages per minute than the first one. But it is important to study the pattern. On the picture, we can see how the number of sausages decreases on each plate. This process is called a decreasing pattern. The second participant ate a plate whole of sausages in five minutes and won!
Cyclic pattern
You know exactly the pattern of this type - this is the change of seasons. Spring-Summer-Autumn-Winter and then it repeats.
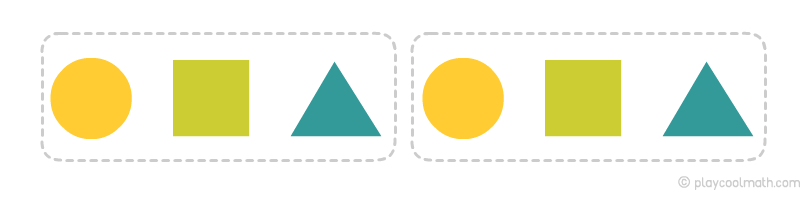
Let’s consider an example with objects of different shapes. On the picture, you see a chain of different numbers of objects. Try to find the pattern in the picture below. Continue the chain.

Subjects are repeated every three cells. If we know the pattern, we can assume which objects will come later. After the last link you will find a triangle, then a circle, then a square.
Complex patterns
Let’s check the example of patterns on the same chain. But we will search for patterns depending on the properties of the links. Try to find the next link in the example below.

Pattern by form
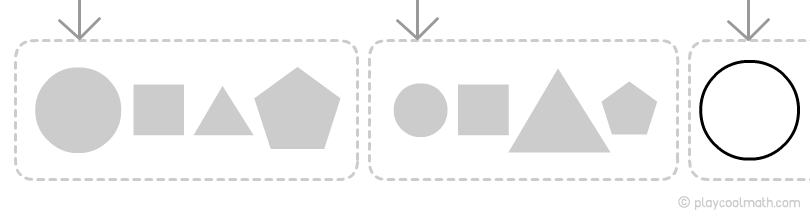
We see how the chain links alternate. We know for sure that a circle will follow by shape. Let’s define it as a large circle.
Pattern by size
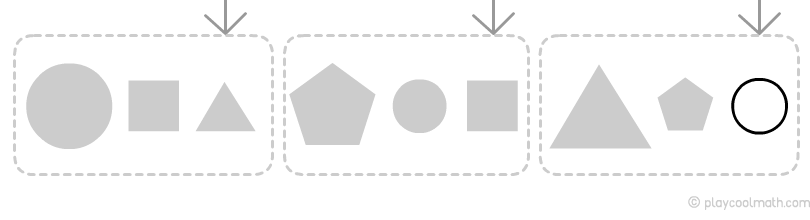
We see how the chain links alternate: big and then two small figures, it means, the next one will be a small figure.
Pattern by color
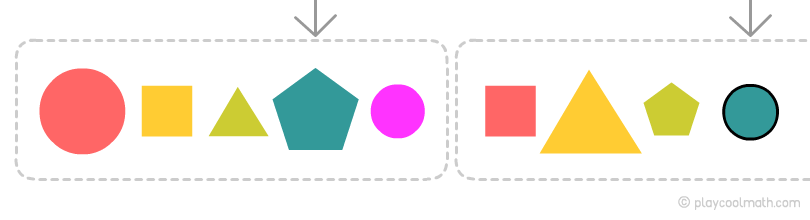
We got the longest pattern in the chain, select it and determine what the next color will be.
As you can see, the pattern depends on the properties of the chain elements. For the same chain, we found different patterns depending on the property. Combine the results and find out which link will be next.

Algorithm for finding patterns
Let's repeat once again all the steps to reveal the patterns.
- Let’s determine the number of properties of the chain;
- Let’s determine the pattern for each property;
- Let’s compare the patterns to determine all the properties of the next link in the chain.
Search for patterns is a very good skill for a young mathematician. In the future, when you study the numbers, you will definitely need this skill. We have created a set of tests where you can practice in the search for patterns. Try to pass all the tests with a good result and move on in the study of maths.


