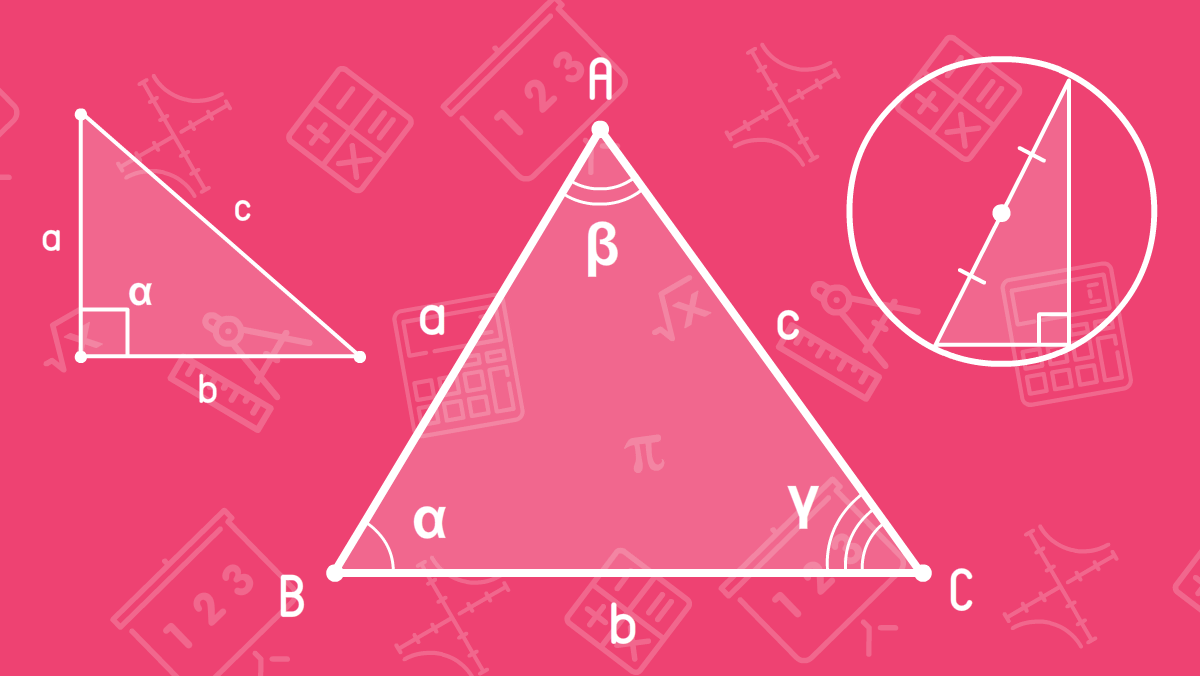
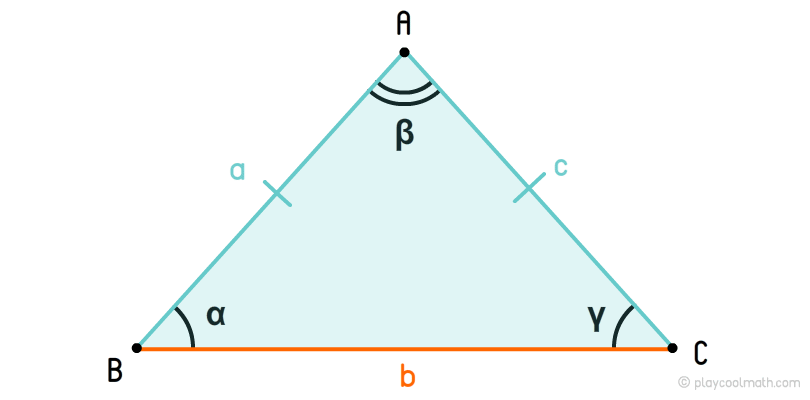
Треугольник - это геометрическая фигура, образованная замкнутой ломаной линией, состоящей из трех отрезков. Точки в треугольнике называются вершинами, отрезки называются сторонами или гранями треугольника.
Взгляни на треугольник и скажи, сколько у треугольника углов? Правильный ответ - три. Поэтому его называют треугольником, так как у него три угла.
Треугольник включает себя такие простейшие фигуры:
- Три точки (A, B, C);
- Три отрезка (AB, BC, AC);
- Три угла (α, β, γ);
- Замкнутая ломаная линия (ABC).
Вершины треугольника
Вершины угла обозначают заглавными латинскими буквами. Треугольник обозначается последовательностью вершин. На рисунке у нас треугольник ABC. Противолежащая грань вершины называется основанием вершины треугольника. На рисунке сторона BC является основанием для вершины A, AC - основание для вершины B и AB - основание для вершины C.
Стороны треугольника
Стороны треугольника (или еще их называют грани или ребра) обозначаются строчными латинскими буквами. На рисунке мы обозначили стороны треугольника буквами a, b, c. Также стороны треугольника можно обозначать в виде отрезков, например a = AB, b = BC, c = AC.
Углы треугольника
Углы, как мы знаем, обозначают строчными греческими буквами. На рисунке углы треугольника обозначены как α, β, γ, где α = BAC, β = ABC, γ = ACB. Каждый угол имеет противолежащую сторону, например углу α соответствует противолежащая сторона BC, углу β - AC и γ - AB.
Классификация треугольников по сторонам
Равносторонний треугольник
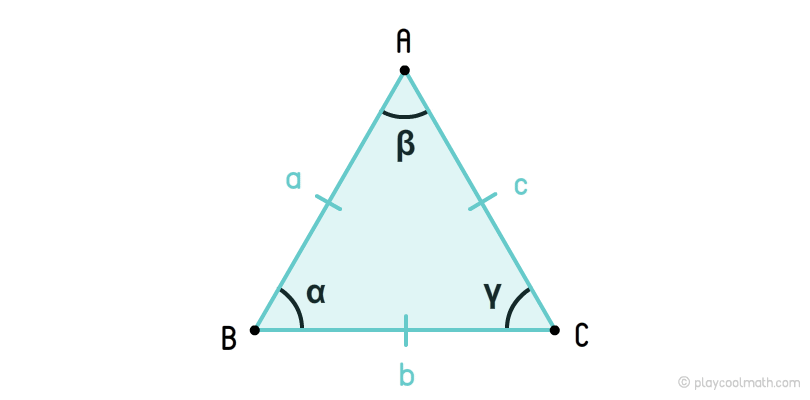
На рисунке мы обозначили стороны как a, b, c, где a = b = c. Углы обозначили как α, β, γ, где α = β = γ = 60°. Одинаковые стороны помечаются одинаковым количеством черточек. Мы пометили стороны a, b, c одной чертой. Одинаковые углы помечаются одинаковым количеством дуг. На рисунке мы все углы пометили одной дугой.
Неравносторонний треугольник
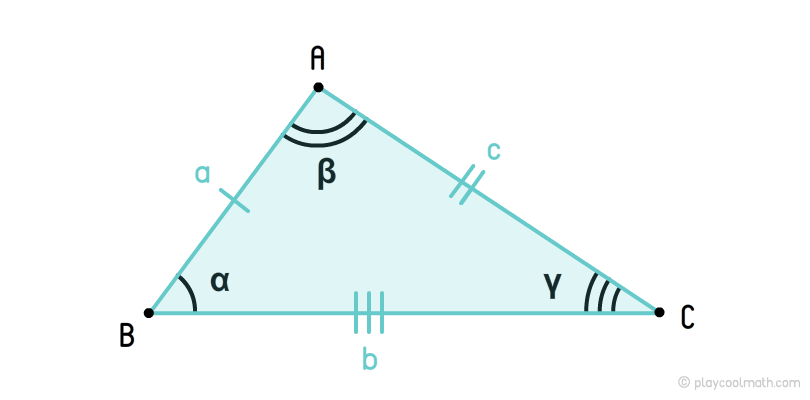
На рисунке мы обозначили стороны a, b, c, где a ≠ b ≠ c. Углы обозначили как α, β, γ, где α ≠ β ≠ γ. Мы пометили стороны a, b, c разным количеством черточек, указав что все стороны имеют разную длину. Все углы пометили разным количеством дуг, указав, что все углы имеют разные угловые меры.
Равнобедренный треугольник
На рисунке мы обозначили боковые стороны как a, c, где a = c, а основание b, где b ≠ a и b ≠ c. У равнобедренного треугольника углы у основания равны α = γ.
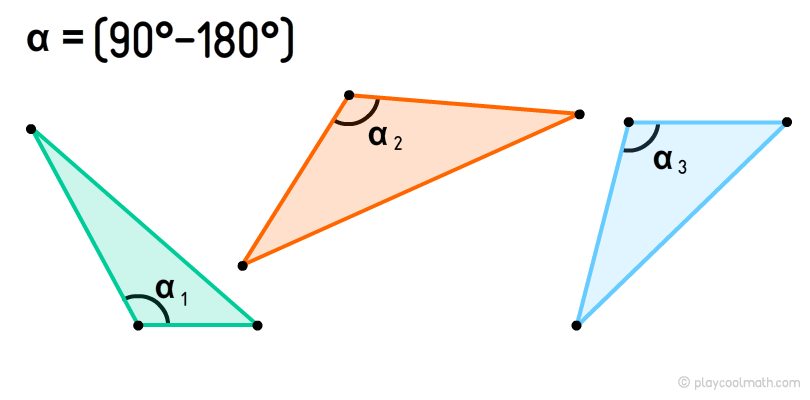
Классификация треугольников по углам
Остроугольный треугольник
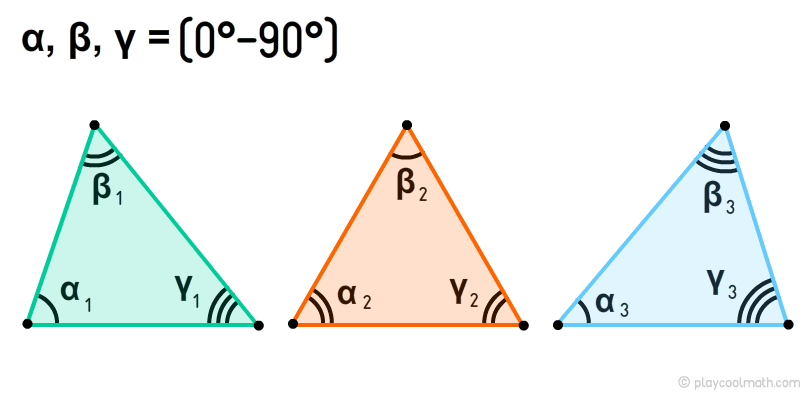
Тупоугольный треугольник
Прямоугольный треугольник
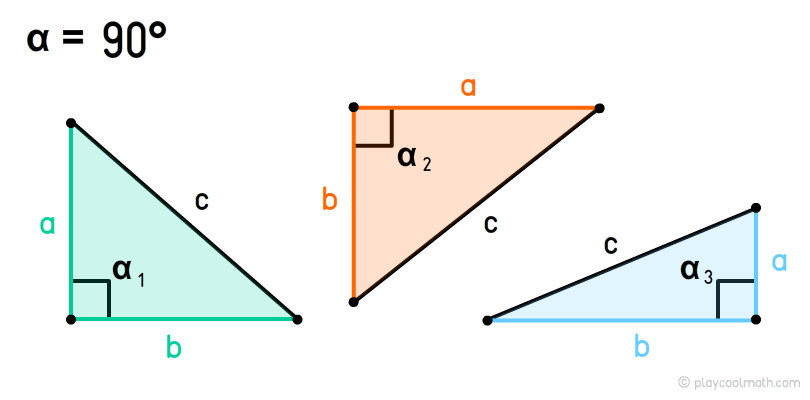
Две стороны образующие прямой угол называются катетами, а сторона, противоположная прямому углу, называется гипотенузой. На рисунке угол α = 90°, сторона a и b - катеты, с - гипотенуза.

Медианы треугольника
То есть медиана разбивает основание на ровных два отрезка. Взгляни на рисунок ниже. Мы нарисовали треугольник с вершиной A и противолежащей для этой вершины стороной a. На отрезке a мы разместили точку D, которая разделяет основания на два равных отрезка BD = DC. Отрезок AB - это медиана для вершины A, a - это основание медианы.
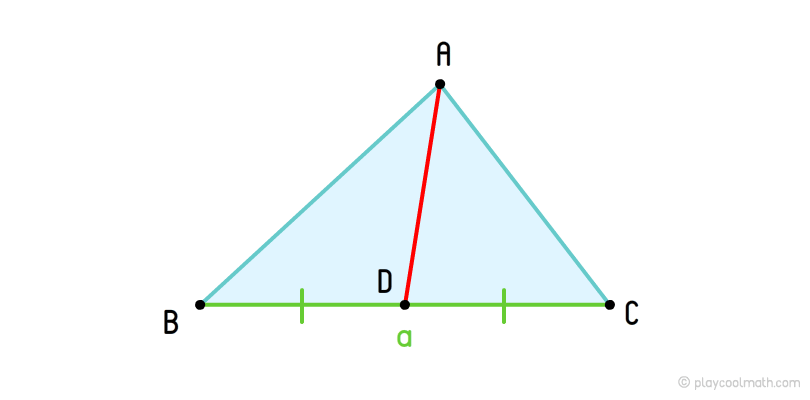
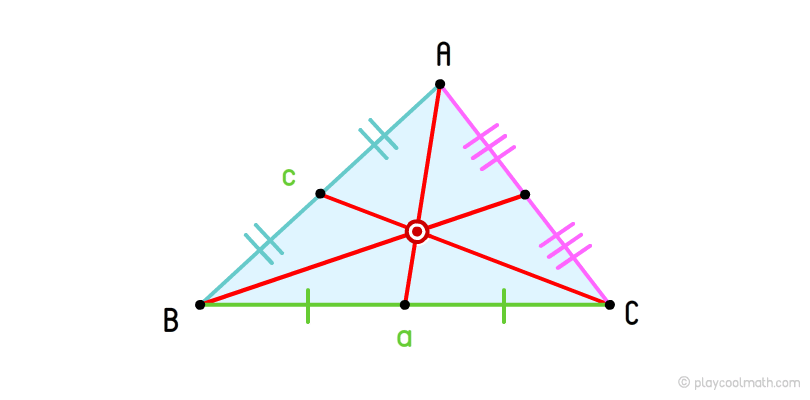
Если нарисовать медианы для всех вершин треугольника, то мы увидим точку пересечения всех медиан - центроид. Центроид делит все медианы на два отрезка в пропорции ½ от основания медианы.
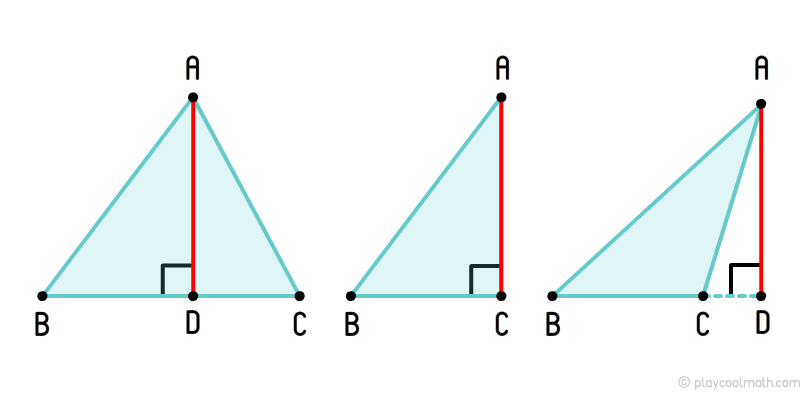
Высота треугольника
На рисунке мы нарисовали разные виды высоты в зависимости от типа треугольника
Точка пересечения всех высот называется ортоцентром. У тупоугольного треугольника ортоцентр лежит за пределами треугольника. У прямоугольного треугольника ортоцентр всегда совпадает с вершиной прямого угла. У равностороннего треугольника медианы и высоты совпадают, соответственно и ортоцентр с центроидом тоже совпадают.
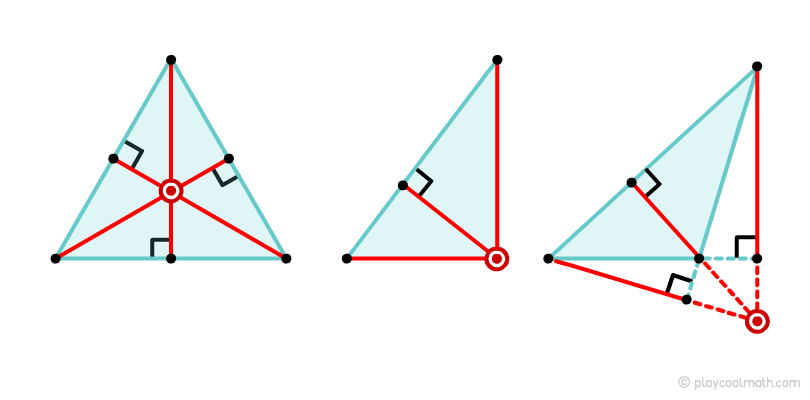
Для того чтобы измерить прямой угол, тебе понадобиться линейка в виде треугольника. Обычно такие линейки имеют три угла 90°, 60°, 30°. Чтобы провести перпендикуляр и нарисовать высоту треугольника, сопоставь одну сторону линейки с любой стороной треугольника так, чтобы вторая сторона прямого угла линейки проходила через высоту этого основания. Посмотри на рисунок ниже, как мы ищем высоту с помощью треугольной линейки.
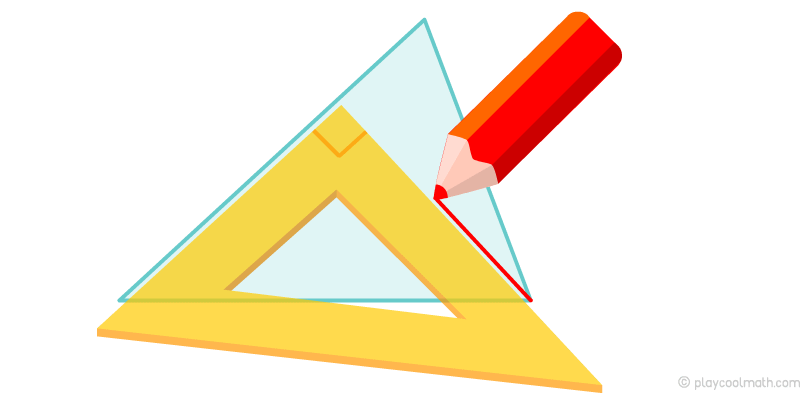
Биссектриса треугольника
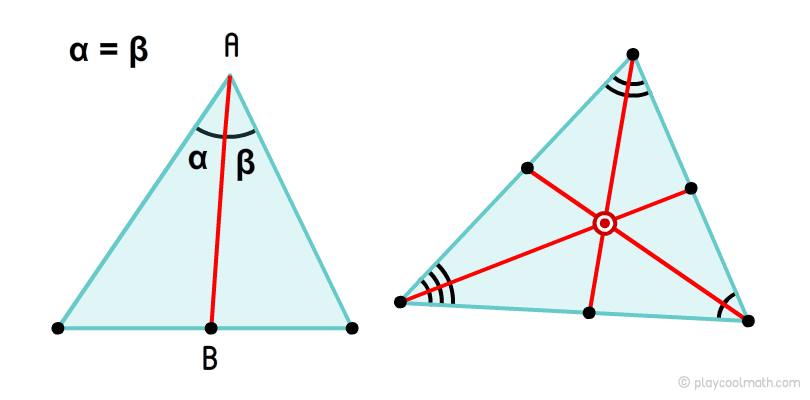
Точка, образованная пересечением биссектрис называется инцентромом.
Для того чтобы измерить угол треугольника и разбить его пополам, тебе понадобится специальная линейка - транспортир. У этой линейки есть шкала, показывающая угловую меру в градусах от центральной точки линейки.
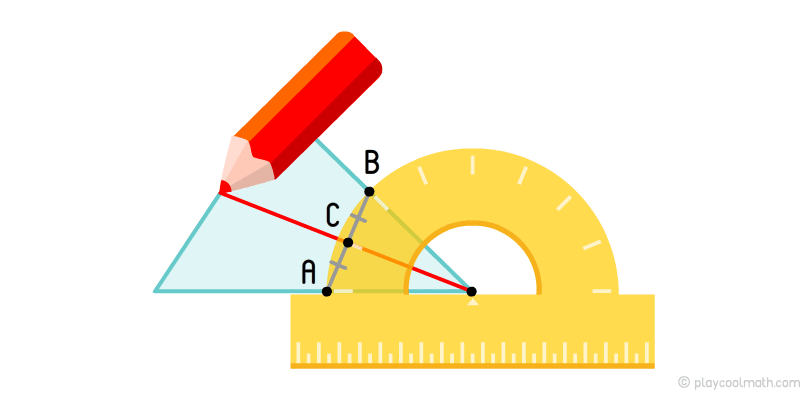
Сопоставь центральную точку линейки с вершиной так, чтобы одна сторона треугольника совпадала с основанием линейки. Найди, на какую цифру, на шкале линейки, указывает вторая сторона вершины, если ее продлить в длину. Поставь точки у значения 0 и там, где мы измерили. Обознач эти точки как A и B.
Проведи отрезок через эти точки. Визуально или с помощью линейки найди середину этого отрезка и обозначь ее как точку C. На линии, проходящей из вершины к точке C, будет лежать наша биссектриса. Повтори все действия для каждой вершины треугольника.
Окружность, вписанная в треугольник
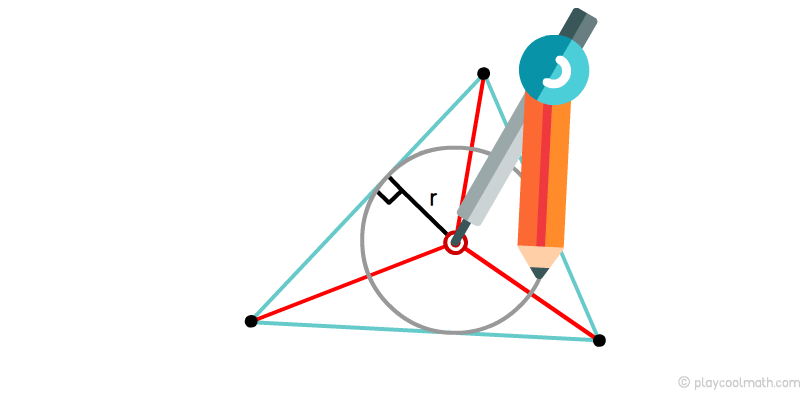
Окружность, касающаяся всех трех сторон треугольника, называется вписанной окружностью. Только одна окружность может быть вписана в любой треугольник.
Центром пересечения биссектрис, как мы знаем, является инцентром. Инцентром еще называют центром вписанной окружности. Если от инцентрома до любого основания измерить расстояние по перпендикуляру, то мы получим радиус вписанной окружности.
Для того, чтобы вписать окружность в треугольник тебе, понадобится циркуль. Выставь циркуль в инцентром и установи радиус равный расстоянию до любого основанию по перпендикуляру. Круговым движением нарисуй окружность.
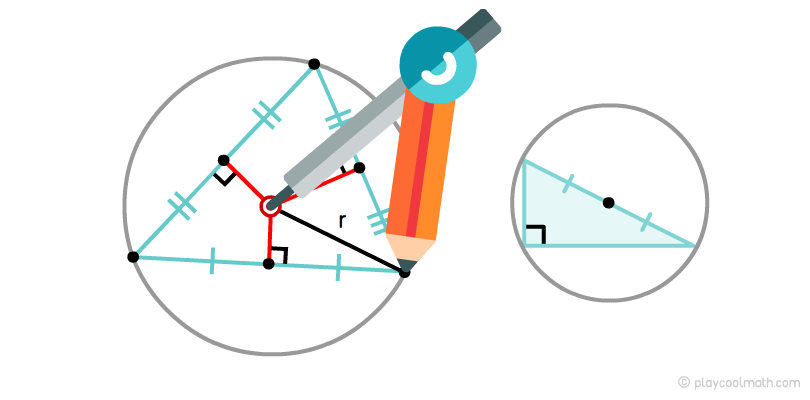
Описанная окружность треугольника
Окружность, проходящая по всем вершинам треугольника, называется описанной окружностью. Любой треугольник может быть описан единственной окружностью.
На рисунке хорошо видно, как из середины оснований мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность.
У прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы.
Найди на рисунке треугольник, который одновременно прямоугольный и равнобедренный.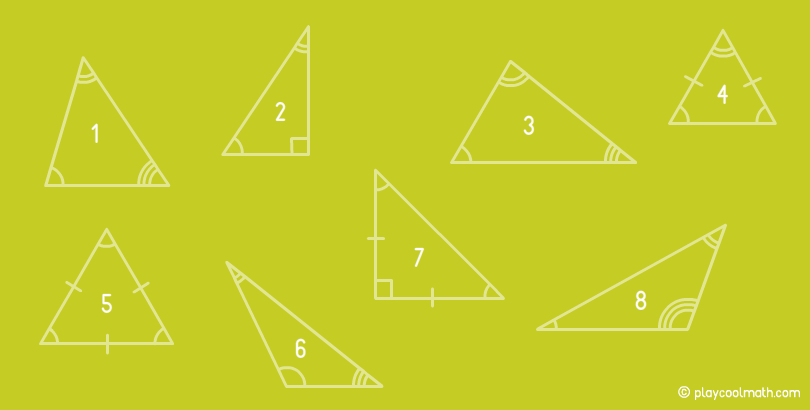
- #7

