Трикутник - це геометрична фігура, утворена замкнутою ламаною лінією, що складається з трьох відрізків. Точки в трикутнику називаються вершинами, відрізки називаються сторонами або гранями трикутника.
Поглянь на трикутник та скажи, скільки у трикутника кутів? Правильна відповідь - три. Тому його називають трикутником, так як у нього три кути.
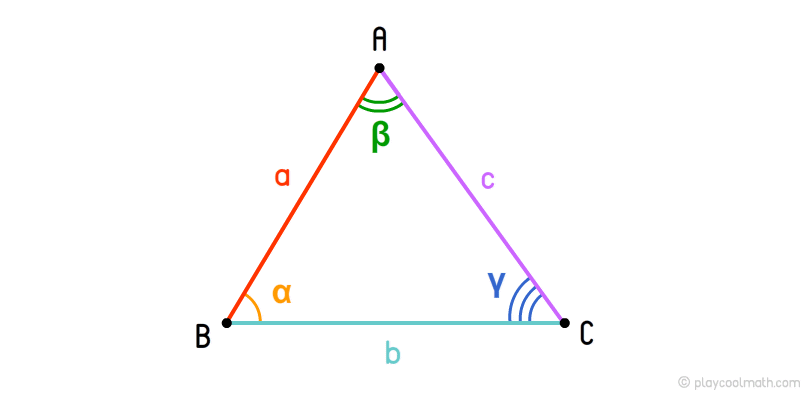
Трикутник включає себе такі найпростіші фігури:
- Три крапки (A, B, C);
- Три відрізка (AB, BC, AC);
- Три кута (α, β, γ);
- Замкнута ламана лінія (ABC).
Вершини трикутника
Вершини кута позначають великими латинськими літерами. Трикутник позначається послідовністю вершин. На малюнку у нас трикутник ABC. Протилежна грань вершини називається підставою вершини трикутника. На малюнку сторона BC є підставою для вершини A, AC - підстава для вершини B та AB - підстава для вершини C.
Стороны трикутника
Сторони трикутника (або ще їх називають грані або ребра) позначаються малими латинськими буквами. На малюнку ми позначили сторони трикутника літерами a, b, c. Також сторони трикутника можна позначати у вигляді відрізків, наприклад a = AB, b = BC, c = AC.
Кути трикутника
Кути, як ми знаємо, позначають малими грецькими буквами. На малюнку кути трикутника позначені як α, β, γ, де α = BAC, β = ABC, γ = ACB. Кожен кут має протилежну сторону, наприклад кутку α відповідає протилежна сторона BC, розі β - AC та γ - AB.
Класифікація трикутників по сторонам
Рівносторонній трикутник
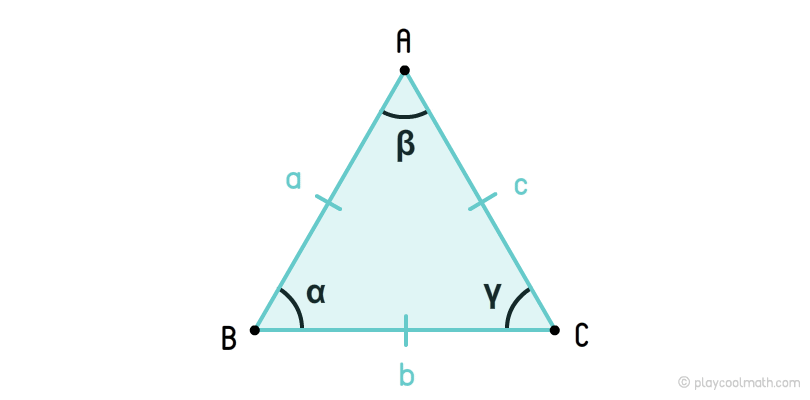
На малюнку ми позначили сторони як a, b, c, де a = b = c. Кути позначили як α, β, γ, де α = β = γ = 60°. Однакові сторони позначаються однаковою кількістю рисок. Ми позначили сторони a, b, c однією рисою. Однакові кути позначаються однаковою кількістю дуг. На малюнку ми всі кути позначили однією дугою.
Нерівносторонній трикутник
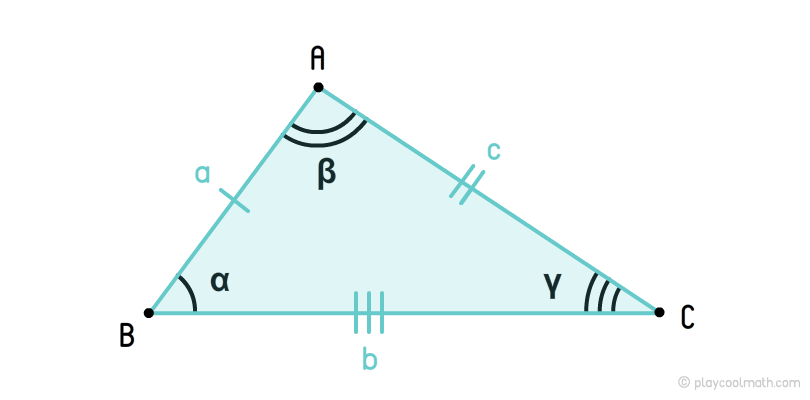
На малюнку ми позначили сторони a, b, c, де a ≠ b ≠ c. Кути позначили як α, β, γ, де α ≠ β ≠ γ. Ми позначили сторони a, b, c різною кількістю рисок, вказавши що всі сторони мають різну довжину. Всі кути позначили різною кількістю дуг, вказавши, що всі кути мають різні кутові міри.
Рівнобедрений трикутник
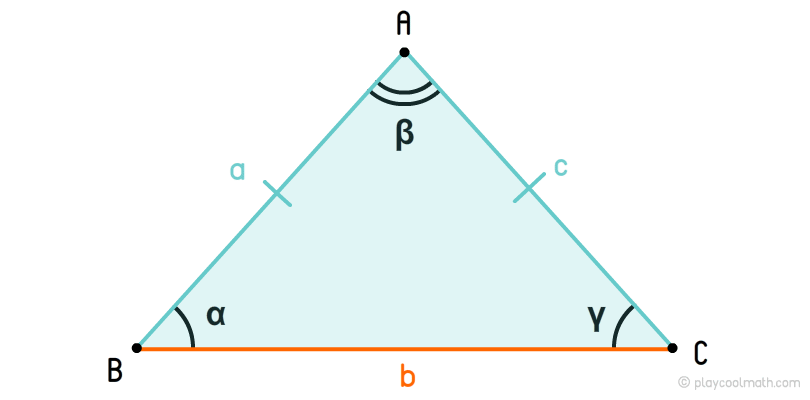
На малюнку ми позначили бокові сторони як a, c, де a = c, а підстава b, де b ≠ a та b ≠ c. У рівнобедреного трикутника кути біля основи рівні α = γ.
Класифікація трикутників по кутах
Гострокутний трикутник
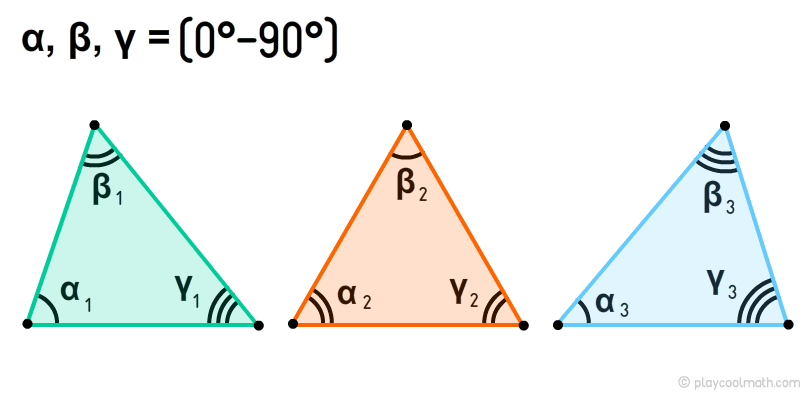
Тупокутний трикутник
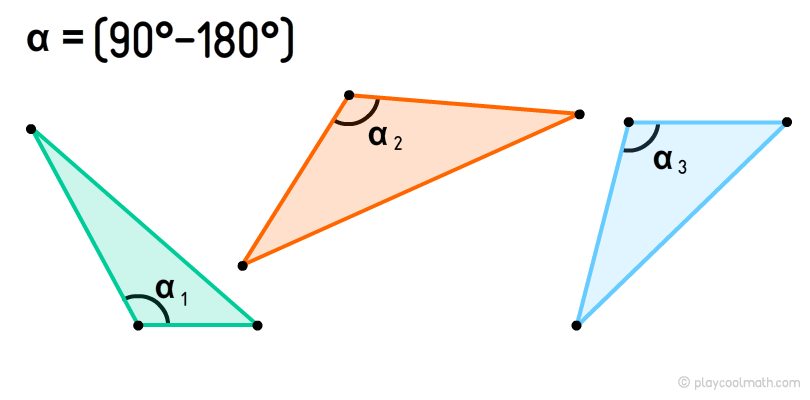
Прямокутний трикутник
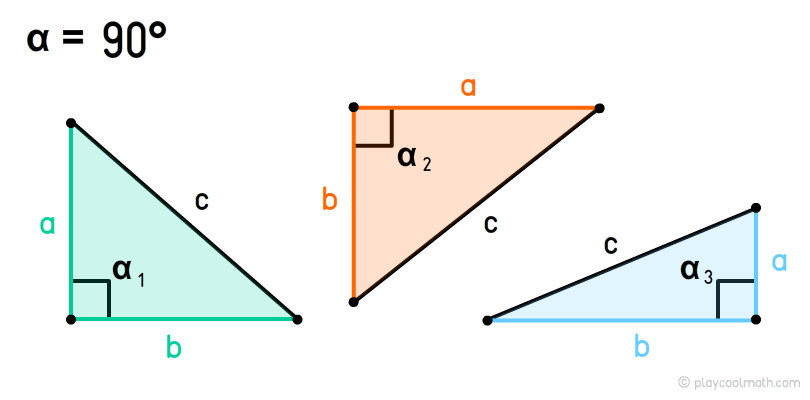
Дві сторони утворюючі прямий кут називаються катетами, а сторона, протилежна прямому куті, називається гіпотенузою. На малюнку кут α = 90°, сторона a та b - катети, с - гіпотенуза.

Медіани трикутника
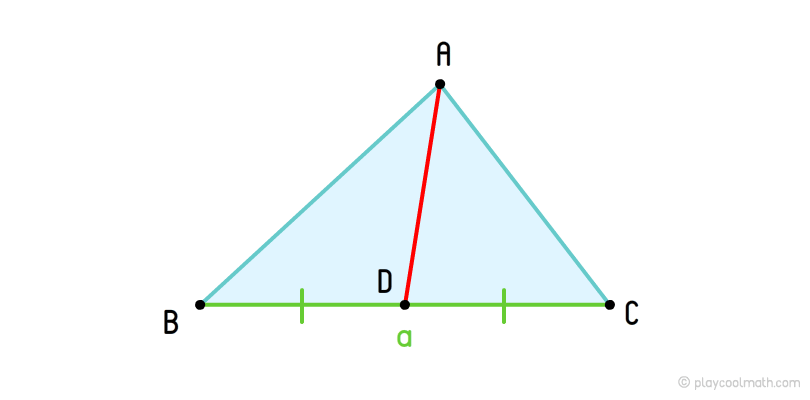
Тобто медіана розбиває підставу на рівних два відрізки. Поглянь на малюнок нижче. Ми намалювали трикутник з вершиною A та протилежною для цієї вершини стороною a. На відрізку a ми розташували точку D, яка розділяє підстави на два рівних відрізка BD = DC. Відрізок AB - це медіана для вершини A, a - це підстава медіани.
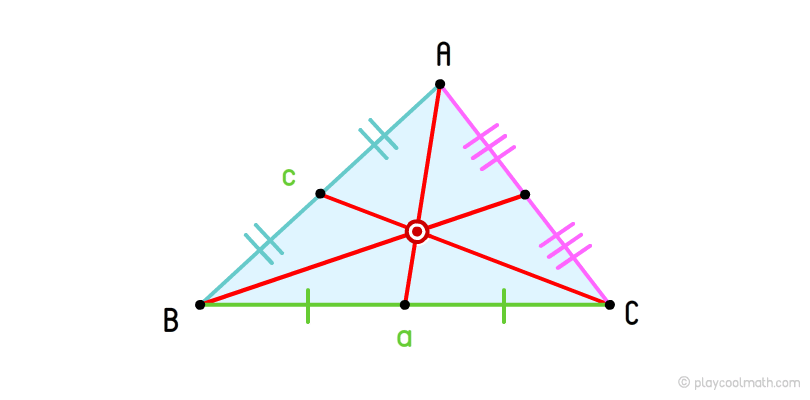
Якщо намалювати медіани для всіх вершин трикутника, то ми побачимо крапку перетину всіх медіан - центроїд. Центроїд поділяє все медіани на два відрізки в пропорції ½ від підстави медіани.
Висота трикутника
На малюнку ми намалювали різні види висоти в залежності від типу трикутника
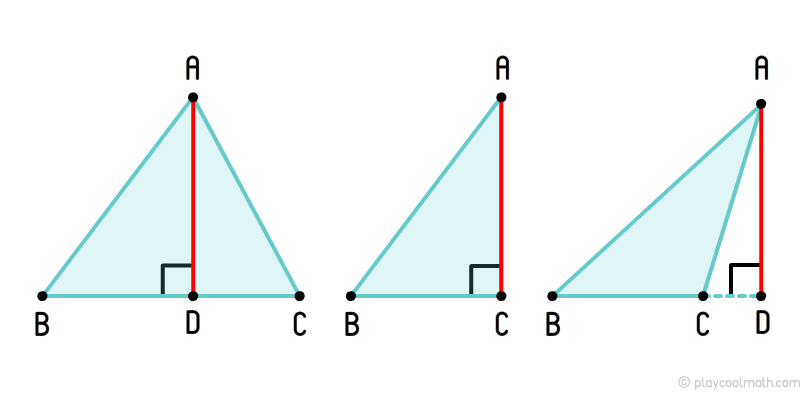
Крапка перетину всіх висот називається ортоцентром. У тупоугольного трикутника ортоцентр лежить за межами трикутника. У прямокутного трикутника ортоцентр завжди збігається з вершиною прямого кута. У рівностороннього трикутника медіани та висоти збігаються, відповідно та ортоцентр з центроїдом теж збігаються.
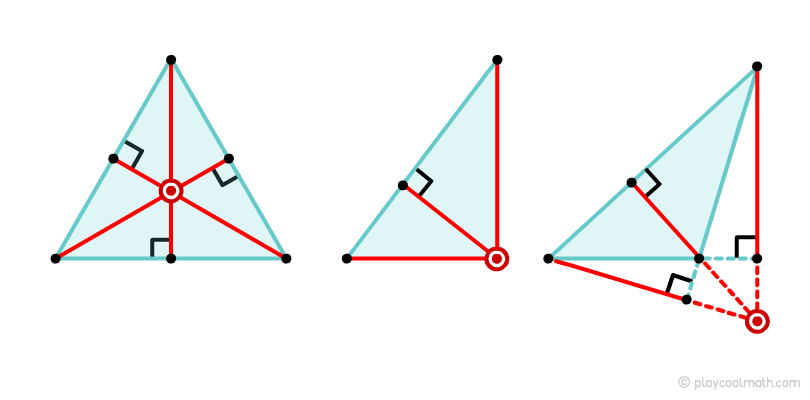
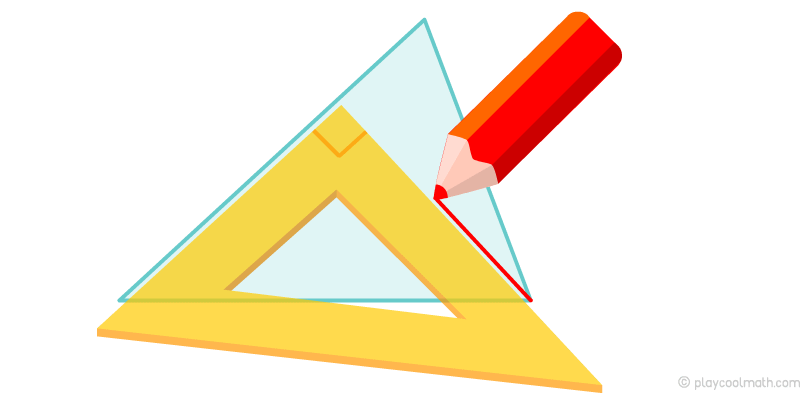
Для того щоб виміряти прямий кут, тобі знадобитися лінійка у вигляді трикутника. Зазвичай такі лінійки мають три кути 90°, 60°, 30°. Щоб провести перпендикуляр та намалювати висоту трикутника, зістав одну сторону лінійки з будь-якою стороною трикутника так, щоб друга сторона прямого кута лінійки проходила через висоту цієї підстави. Подивися на малюнок нижче, як ми шукаємо висоту за допомогою трикутної лінійки.
Бісектриса трикутника
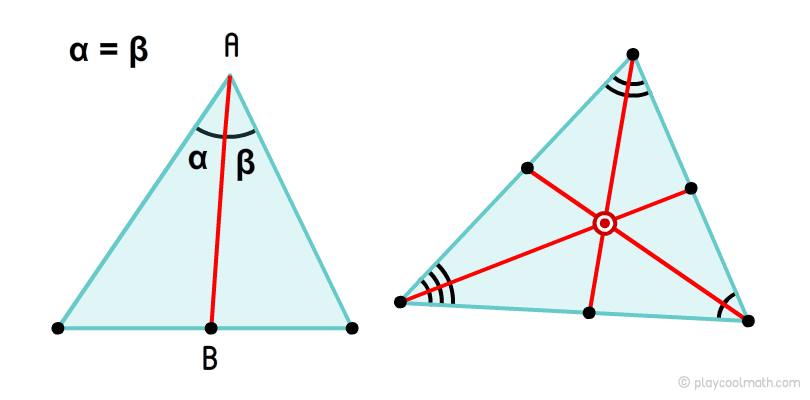
Крапка, утворена перетином биссектрис називається інцентромом.
Для того щоб виміряти кут трикутника та розбити його навпіл, тобі знадобиться спеціальна лінійка - транспортир. У цієї лінійки є шкала, що показує кутову міру в градусах від центральної крапки лінійки.
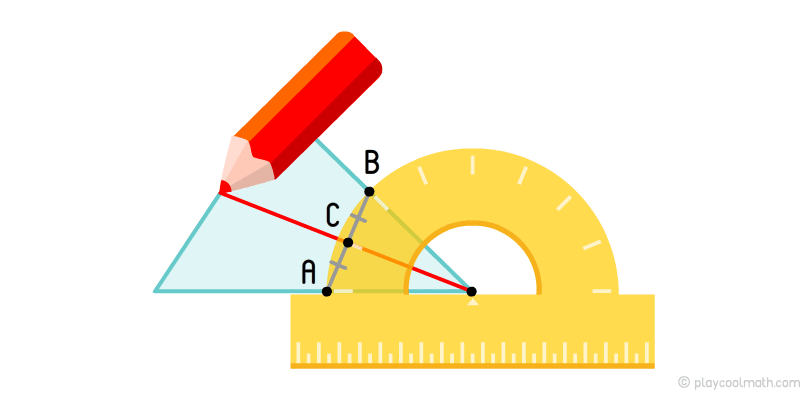
Зістав центральну крапку лінійки з вершиною так, щоб одна сторона трикутника збігалася з підставою лінійки. Знайди, на яку цифру, на шкалі лінійки, вказує друга сторона вершини, якщо її продовжити в довжину. Постав крапки у значення 0 та там, де ми виміряли. Познач ці крапки як A та B.
Проведи відрізок через ці крапки. Візуально або за допомогою лінійки знайди середину цього відрізка та познач її як крапку C. На лінії, що проходить з вершини до точки C, буде лежатиме наша бісектриса. Повторіть всі дії для кожної вершини трикутника.
Коло, вписане в трикутник
Коло, що торкається всіх трьох сторін трикутника, називається вписаним колом. Тільки одне коло може бути вписанє в будь-який трикутник.
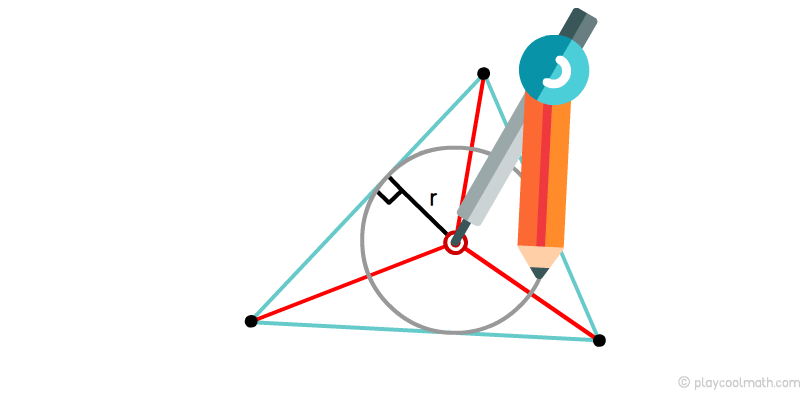
Центром перетину биссектрис, як ми знаємо, є інцентром. Інцентром ще називають центром вписаного кола. Якщо від інцентрома до будь-якого підстави виміряти відстань по перпендикуляру, то ми отримаємо радіус вписаного кола.
Для того, щоб вписати коло в трикутник тобі, знадобиться циркуль. Постав циркуль в інцентром та встанови радіус що дорівнює відстані до будь-якої підстави по перпендикуляру. Круговим рухом намалюй коло.
Описане коло трикутника
Коло, що проходить по всіх вершин трикутника, називається описаним колом. Будь який трикутник може бути описан єдиним колом.
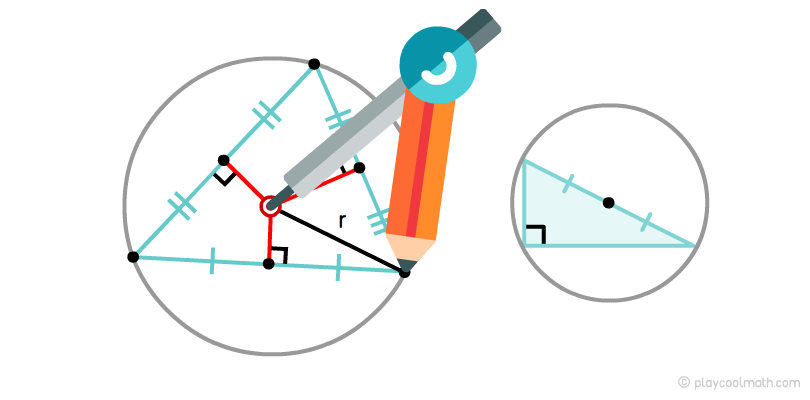
На малюнку добре видно, як з середини підстав ми провели перпендикуляри та знайшли крапку перетину. За допомогою штангенциркуля виставляємо радіус від центру до будь-якої вершини та круговим рухом малюємо описане коло.
У прямокутного трикутника центр описаного кола лежить на середині гіпотенузи.
Знайди на малюнку трикутник, який одночасно прямокутний та рівнобедрений.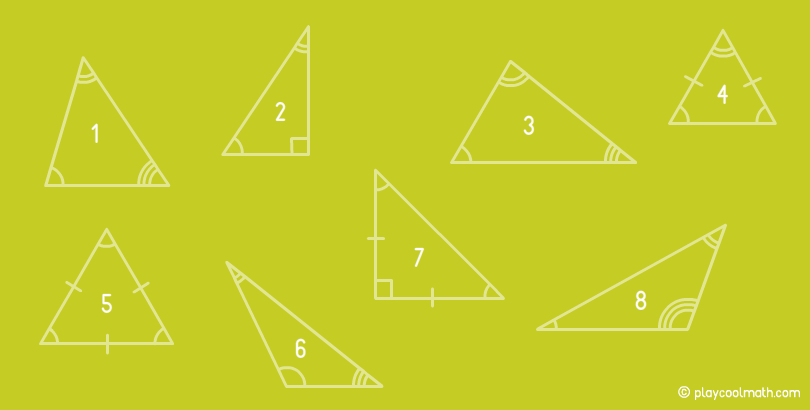
- #7

