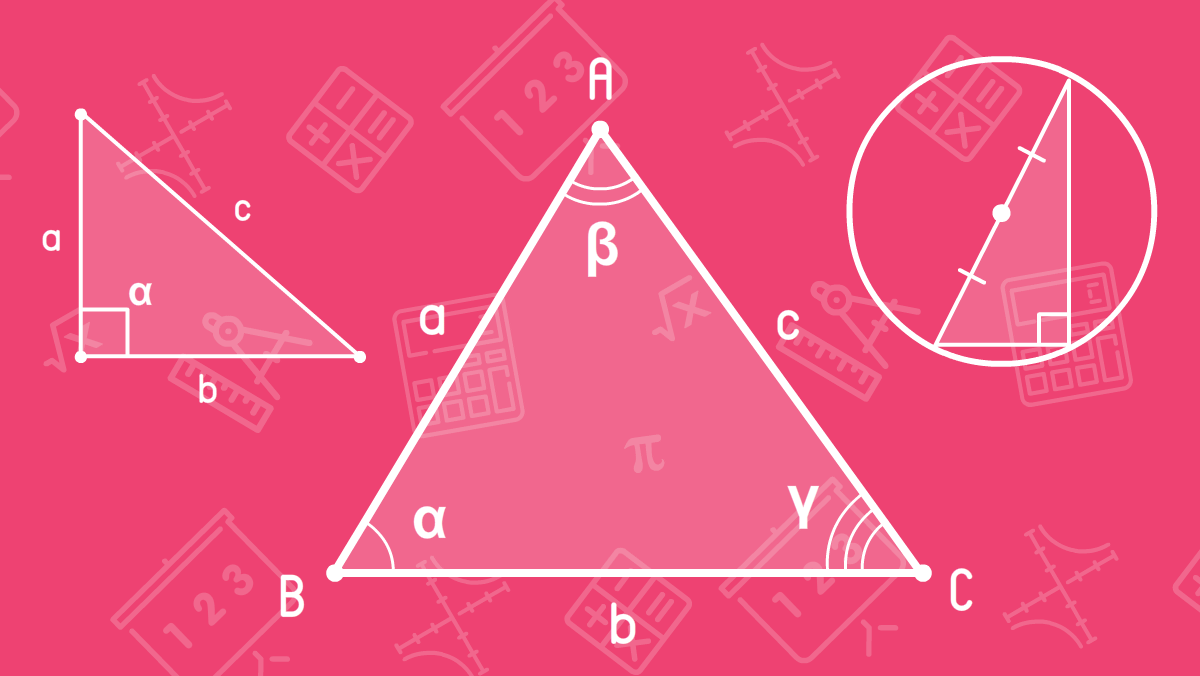
A triangle is a geometric shape created by a closed broken line that consists of three segments. The points in the triangle are called vertices, the segments are called the sides or, in other words, edges of the triangle.
Take a look at the triangle and tell me how many angles does it have? The correct answer is three. That is why it is called a triangle because it has three angles.
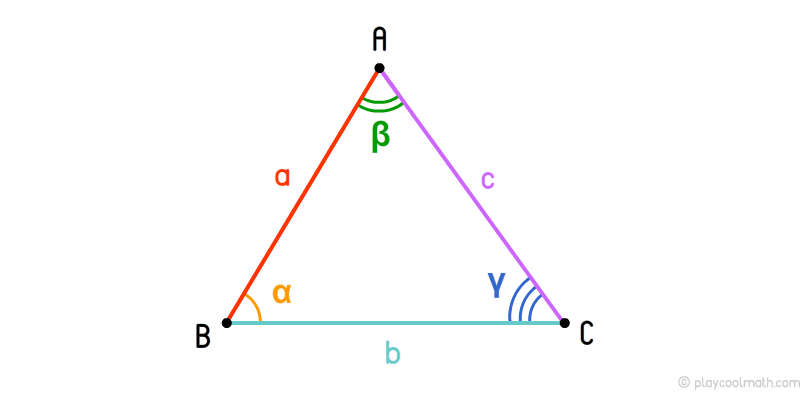
The triangle includes the following simple shapes:
- Three points (A, B, C);
- Three segments (AB, BC, AC);
- Three angles (α, β, γ);
- A closed broken line (ABC).
Triangle vertices
The tops of the angle are defined in capital latin letters. The triangle is determined by a sequence of its vertices. In the picture we can see the triangle ABC. The opposite face of a vertex can be defined the base of the vertex of a triangle. In the figure, BC represents the base for the vertex A, AC is the base for the vertex B and AB is the base for the vertex C.
Triangle sides
The sides of the triangle (or else they are called faces or edges) are defined by lowercase Latin letters. In the figure, we marked triangle sides with letters a, b, c. Also, the sides of a triangle can be determined as segments, for example, a = AB, b = BC, c = AC.
Triangle angles
Angles, as we know, are defined by lowercase Greek letters. In the picture, the angles of the triangle are determined by α, β, γ, where α = BAC, β = ABC, γ = ACB. Every angle has an opposite side, for example, the opposite side BC, the angle β - AC and γ - AB correspond to the angle α.
Classification of triangles by their sides
Equilateral triangle
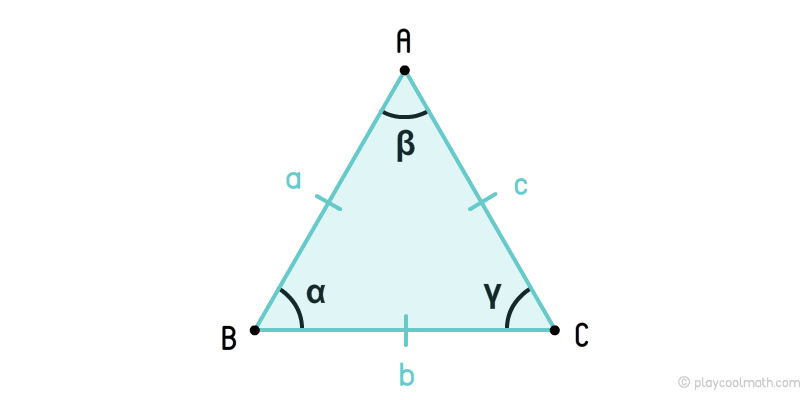
In the picture, we determined the sides as a, b, c where a = b = c. The angles marked as α, β, γ where α = β = γ = 60°. Same angles are marked with the same amount of dashes. We marked the sides a, b, c with one line. The same angles are marked with the same number of arcs. In the picture, all the angles are marked with one arc.
Non-equilateral triangle
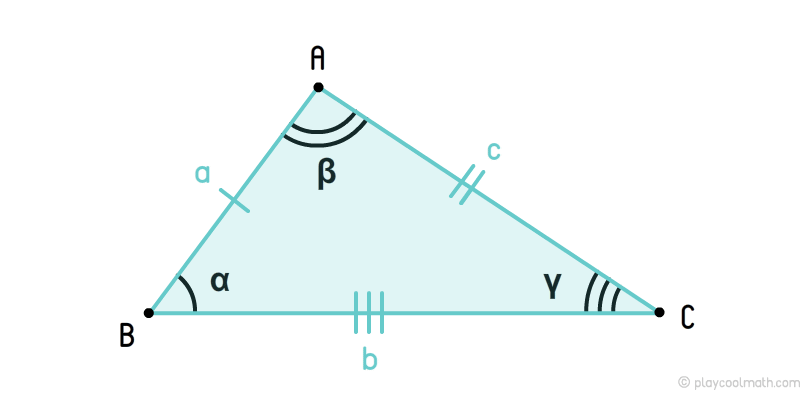
In the picture, we marked sides a, b, c where a ≠ b ≠ c. The angles were defined as α, β, γ, where α ≠ β ≠ γ. We marked the sides a, b, c with a different number of dashes assuming that all the sides are different in length. All angles were marked with a different number of arcs, indicating that all angles have different angular measures.
Isosceles triangle
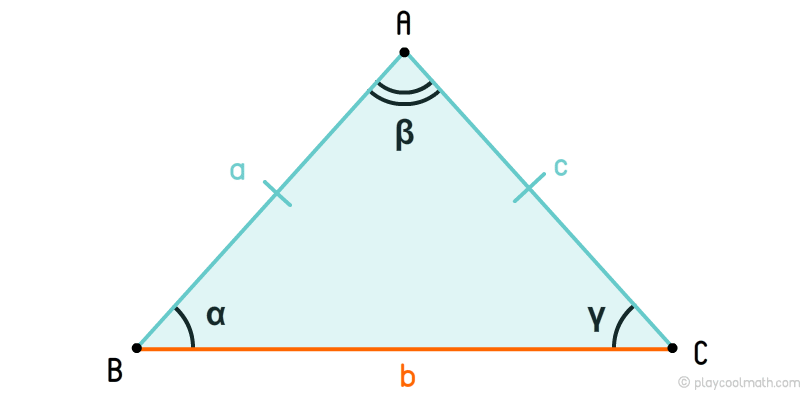
The picture shows sides as a, c where a = c, and the base b where b ≠ a and b ≠ c. An isosceles triangle has the angles at the base marked as α = γ.
Classification of triangles by angles
Acute-angled triangle, or acute triangle
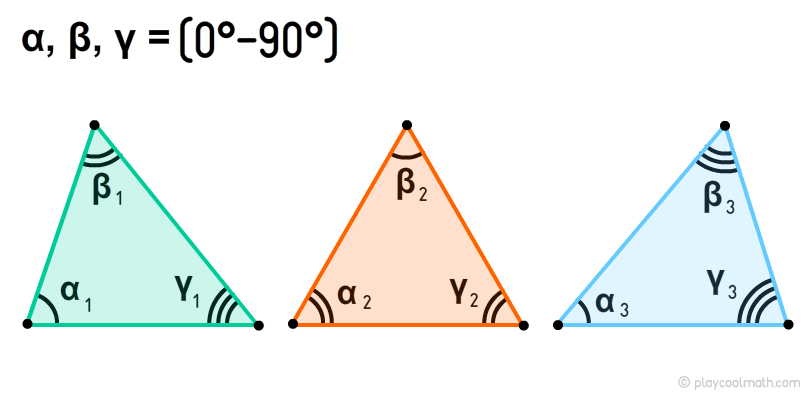
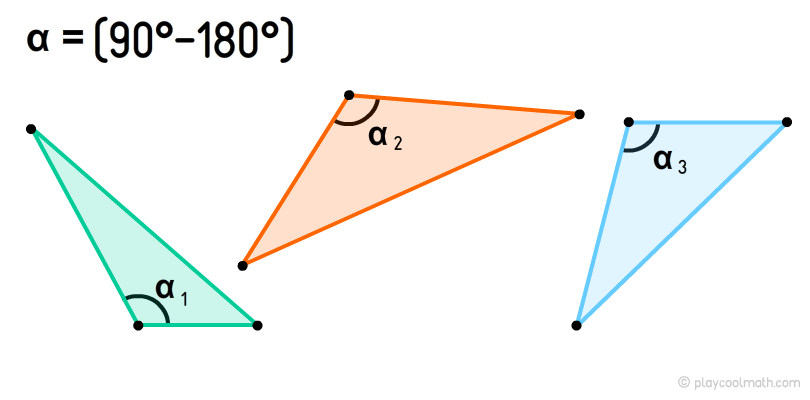
Obtuse-angled triangle, or obtuse triangle
Right-angled triangle, or right triangle
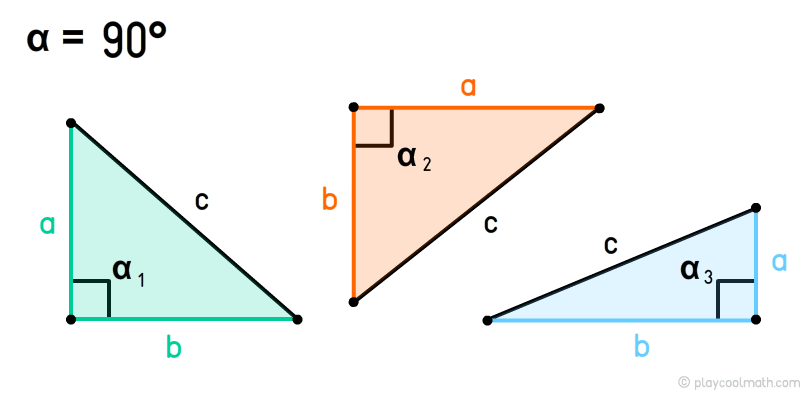
The two sides making the right angle are called the legs, and the side opposite the right angle is called the hypotenuse. In the picture, the angle α = 90°, the side a and b are legs, с is hypotenuse.

Triangle medians
That is, the median breaks the ground into two equal segments. Take a look at the picture below. We have drawn a triangle with vertex A and opposite side for this vertex a. On the following segment A we placed the point D, dividing the bases into two equal segments BD = DC. The segment AB is the median for the vertex A, and a is the base of the median.
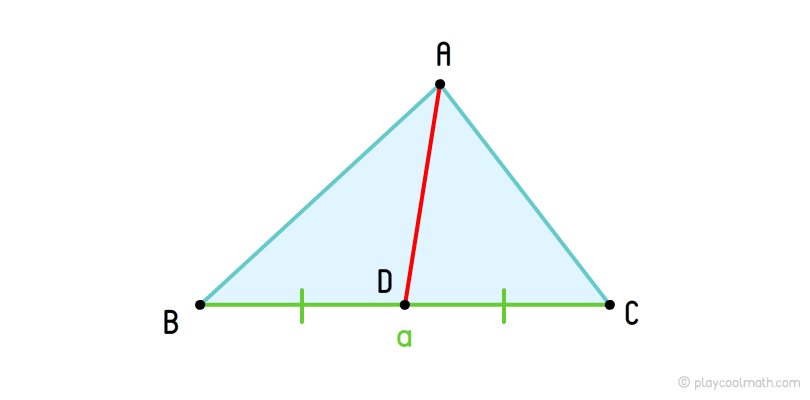
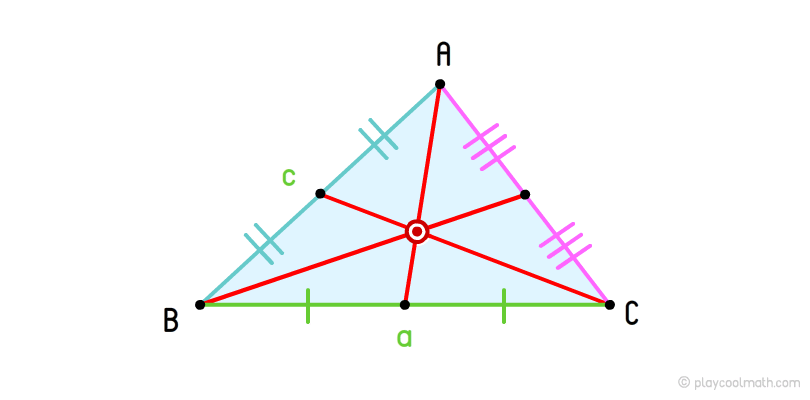
If we draw medians for all vertices of the triangle, we will see the intersection point of all medians that is called centroid. The centroid divides all medians into two segments equal of ½ from the base of the median.
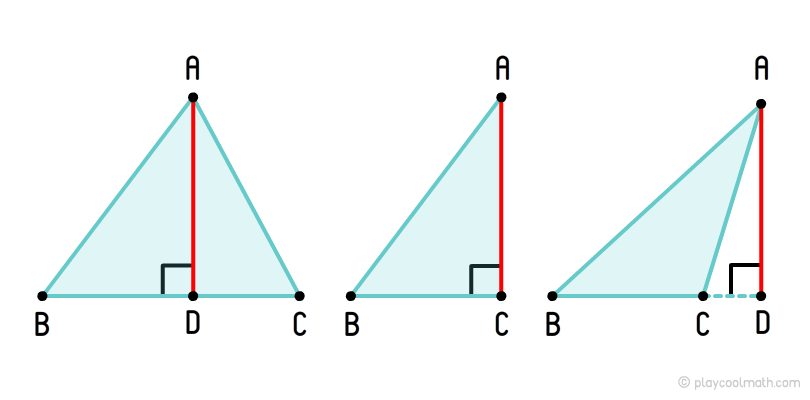
Triangle height
In the picture below, we have drawn different types of height based on the type of triangle.
The point of the intersection of all the heights is the orthocentre. An obtuse triangle has the orthocenter outside the triangle. In a right triangle, the orthocenter always correlates with the vertex of a right angle. An equilateral triangle has the medians and altitudes coinciding and the orthocenter with the centroid also correlate.
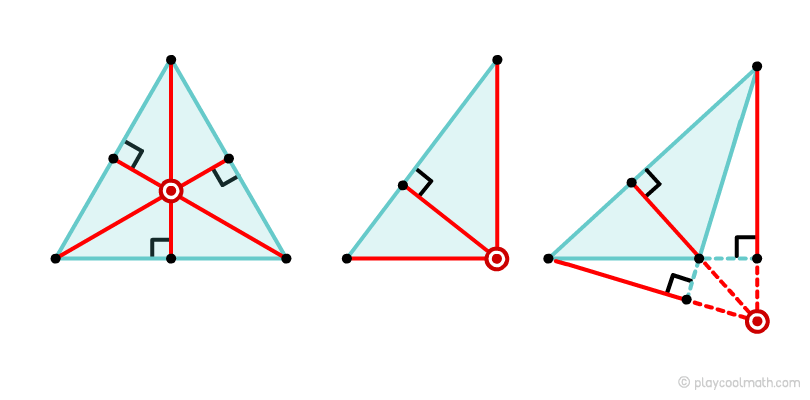
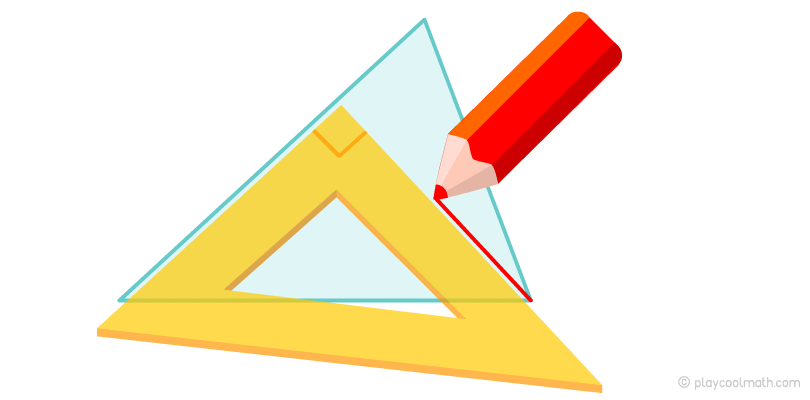
To measure the right angle, you should have a ruler in the shape of a triangle. Usually such rulers have got three angles of 90°, 60°, 30°. In order to draw a perpendicular and draw the height of the triangle, match one side of the ruler to either side of the triangle so that the second side of the right angle of the ruler goes through the height of this triangle. Look at the picture below, as we look for height using a triangular ruler.
Triangle bisector
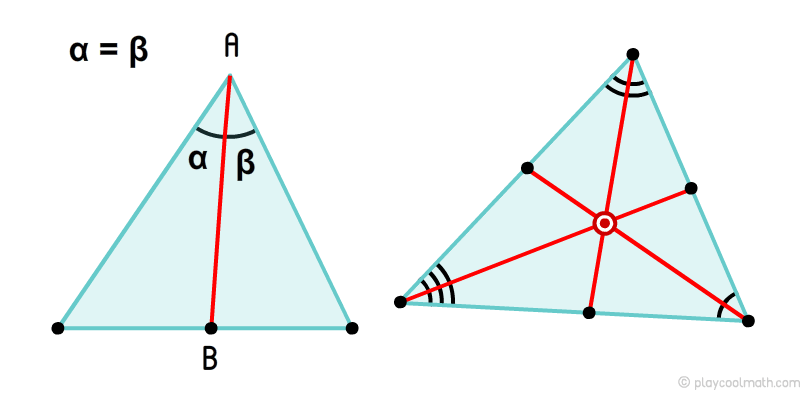
The point formed by the intersection of bisectors is called the incenter.
To measure the angle of the triangle and split it in half, you will need a special ruler – a protractor. This ruler has a scale showing the angular measure in degrees from the central point of the ruler.
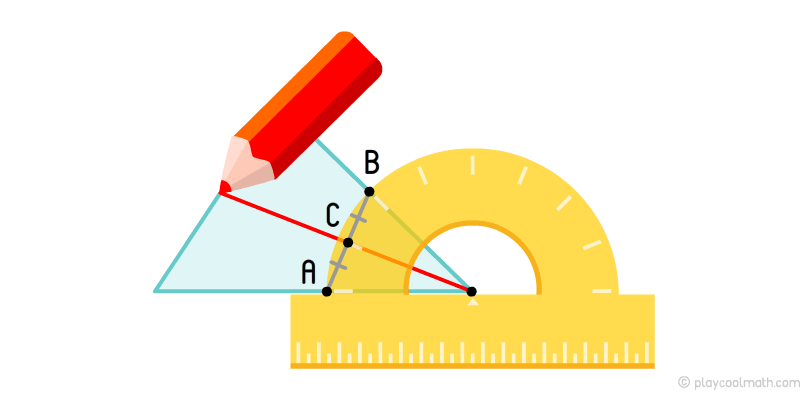
Match the central point of the ruler to the vertex so that one side of the triangle coincides with the base of the ruler. Find on which number indicates the second side of the top indicates if it is extended in length. Set the points at the value 0 and where we measured. Mark these points as A and B.
Make a line through these points. Visually or using a ruler, find the middle of this segment and mark it as point C. On the line passing from the vertex to the point C, you will find our bisector will lie. Repeat all the steps for each vertex of the triangle.
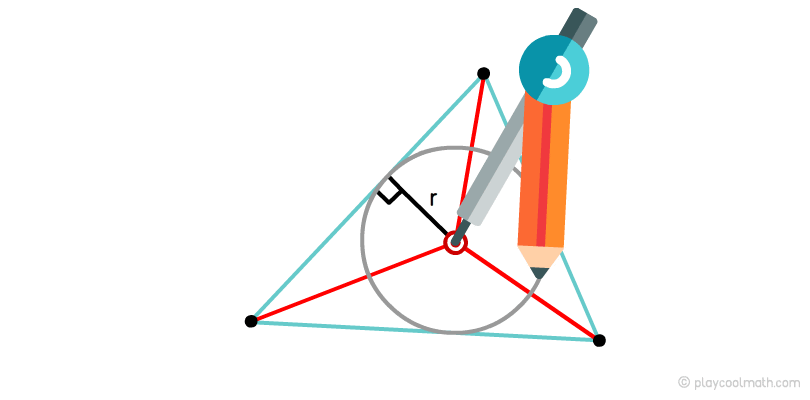
A circle inscribed in a triangle
A circle tangent to all three sides of a triangle is called an inscribed circle. Only one circle can be inscribed in any triangle.
The center of intersection of bisectors is an incenter. The incenter is also called the center of the inscribed circle. If we measure the perpendicular distance from an intentrometer to any base, we get the radius of the inscribed circle.
To inscribe a circle in a triangle to you, you need a compass. Put the compass in the center and set the radius equal to the distance to any base on the perpendicular. With a circular motion draw a circle.
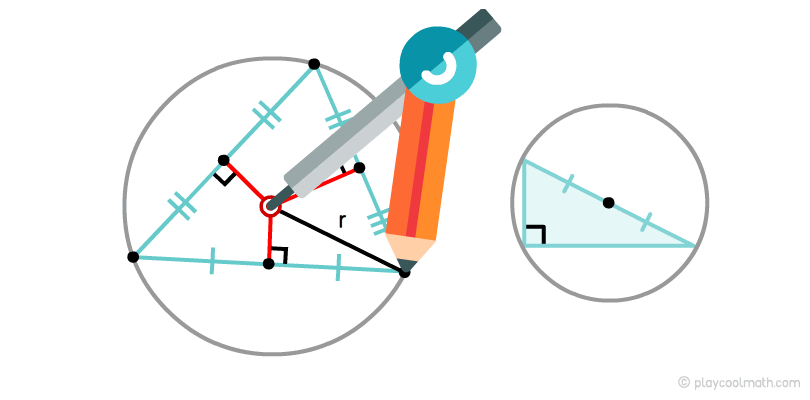
Circumscribed circle of the triangle
A circle going through all the vertices of a triangle is called the circumscribed circle. A triangle can be described by a single circle.
The shape shows clearly how from the middle of the bases we have drawn perpendiculars and found the point of intersection. With the help of the caliper, we expose the radius from the center to any vertex and with a circular motion draw the circumscribed circle.
A right-angled triangle has a center of the circumscribed circle in the middle of the hypotenuse..
In the picture below, find a triangle that is both rectangular and isosceles.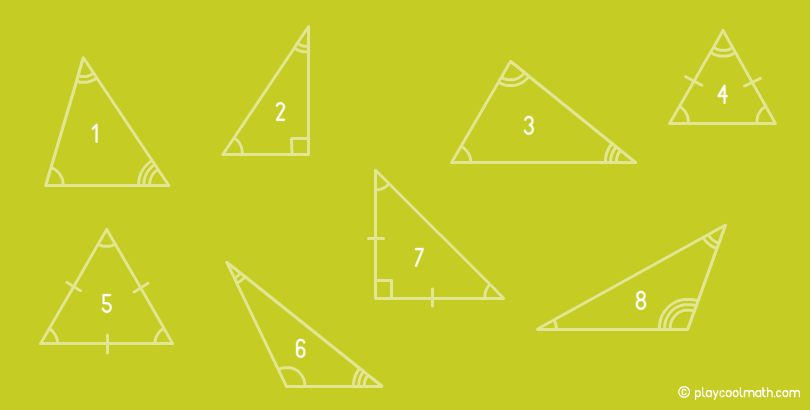
- #7

