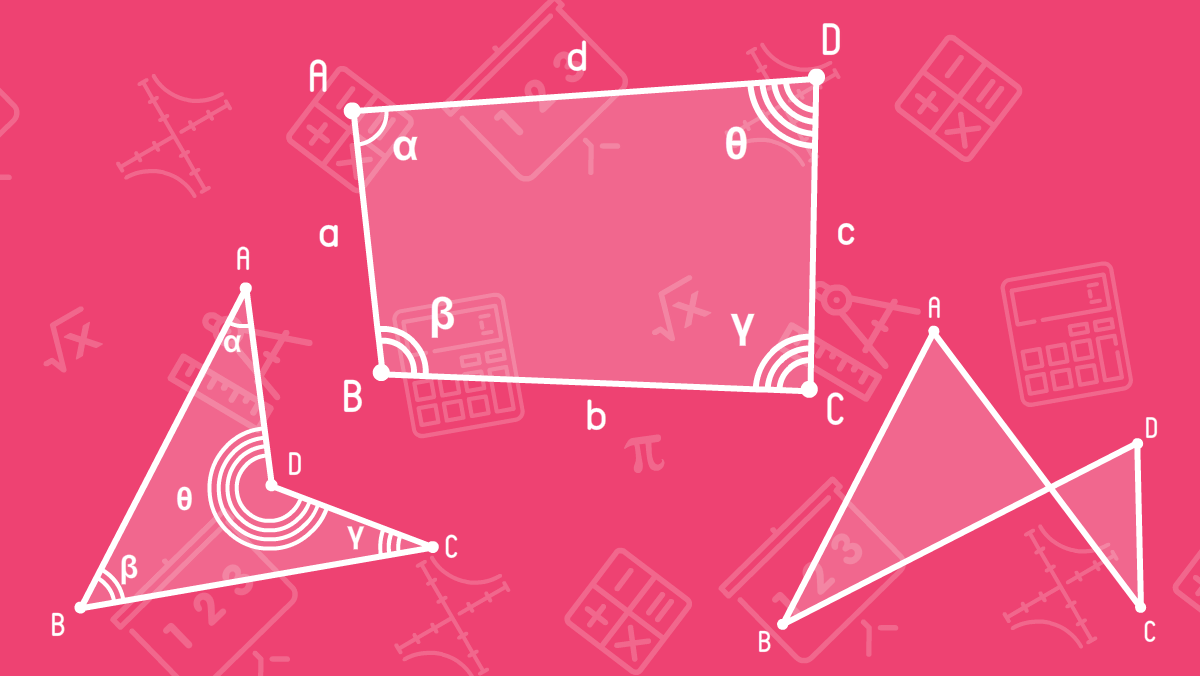
In the previous lesson we learnt about triangles. Now we know what triangles can be and how they differ from each other as well as what common features all triangles have. In this lesson, we will learn what a quadrangle is. Let's begin our lesson with the definition of a quadrangle.
The quadrangle includes the following simple figures:
- Four points (A, B, C, D);
- Four segments (AB, BC, CD, DA);
- Four corners (α, β, γ, θ);
- A closed broken line (ABCD).
Vertices of the quadrangle
The vertices of the quadrangle are defined with capital Latin letters. The quadrangle is denoted by a sequence of vertices. In the image we have the quadrangle ABCD.
Sides of the quadrangle
The sides of the quadrangle (or so-called faces or edges) are denoted by lowercase Latin letters. In the image, we have designated the sides of the quadrangle with letters a, b, c, d. Also, triangle sides can be defined as segments, for example, a = AB, b = BC, c = CD, d = DA. Sides belonging to the same vertex are called adjacent parties. In the image for the vertex A we have adjacent sides AD and AB.
Quadrangle angles
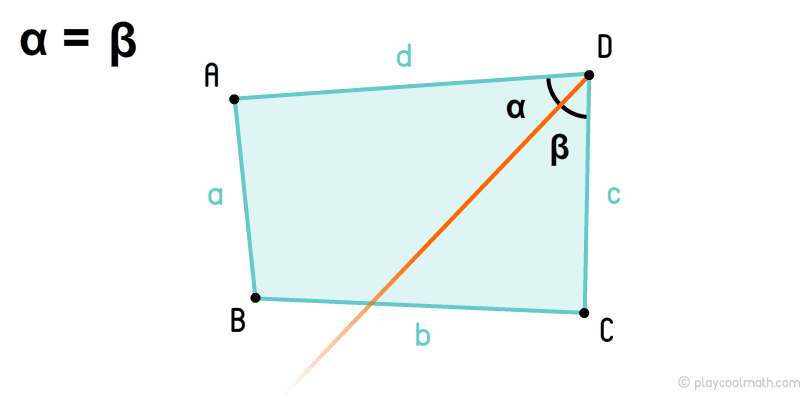
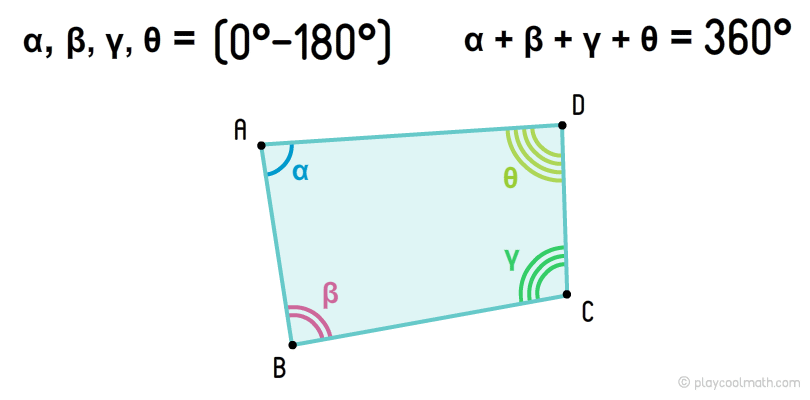
As we know, the angles are defined with lowercase Greek letters. In the image, the angles of the quadrangle are denoted by α, β, γ, θ, where α = DAB, β = ABC, γ = BCD, θ = CDA. Each corner of the quadrangle has an opposing angle, for example, in the figure the angle α has an opposing angle γ, and for β the opposite angle θ.
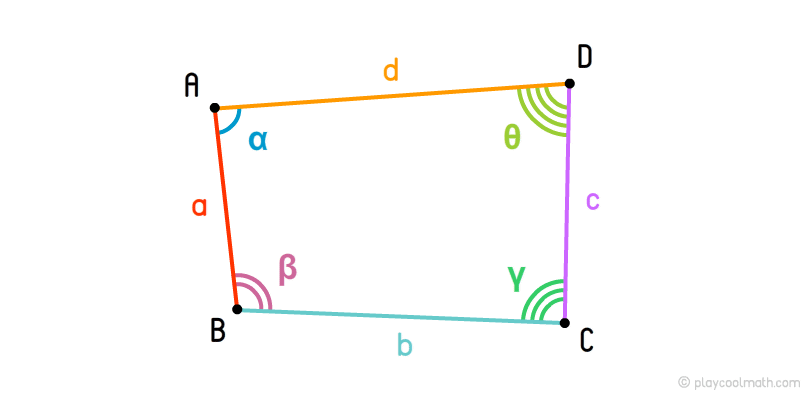
Quadrangle diagonals
Overall, the quadrangle has two diagonals. In the image, segments AC and BD are the diagonals of the quadrangle ABCD.
If quandrangle diagonals intersect at a right angle, it is called orthodiagonal.
Quadrangle bisectors
During the lesson about triangles, we described how a bisector of a vertex can be found with the help of a protractor.
Quadrangle middle lines
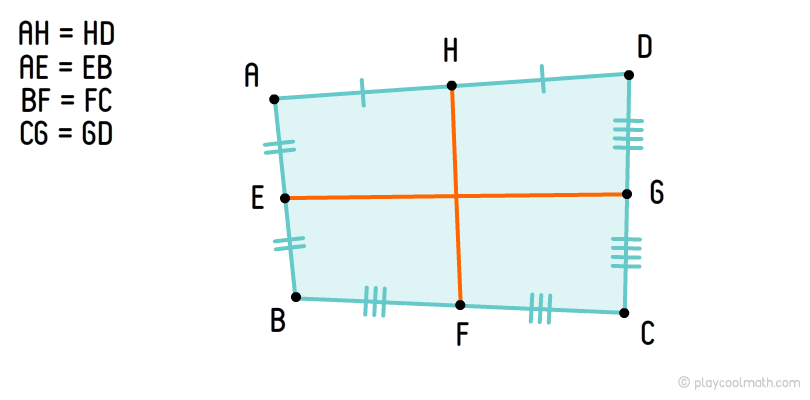
In order to draw the middle line, you need to split all sides of the quadrangle into two equal segments and to find the midpoints. The midpoints of the opposite sides must be joined by segments that will be quadrangle middle lines.
Classification of quadrangles
Convex quadrangles
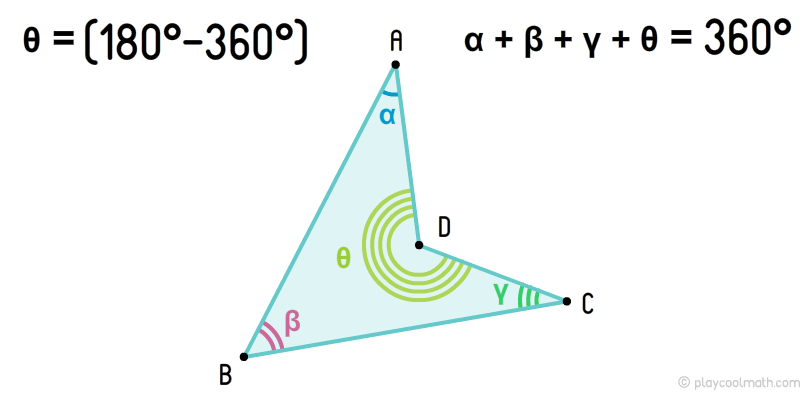
Non convex or concave quadrangles
Self-intersecting quadrangles
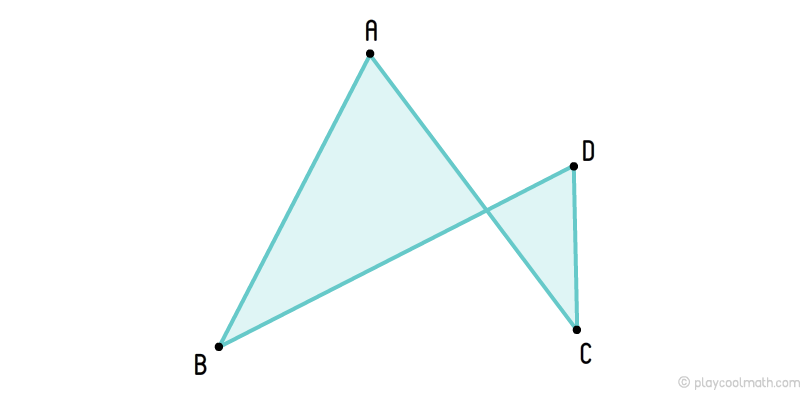
A quadrangle that is visually self-intersecting is similar to two triangles with the sides that lie on two intersecting lines, and their intersection point is a common vertex for triangles.
Types of quadrangles and their features
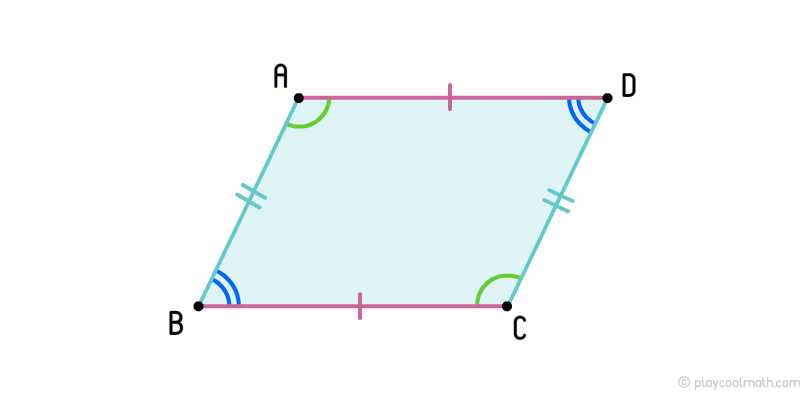
Parallelogram
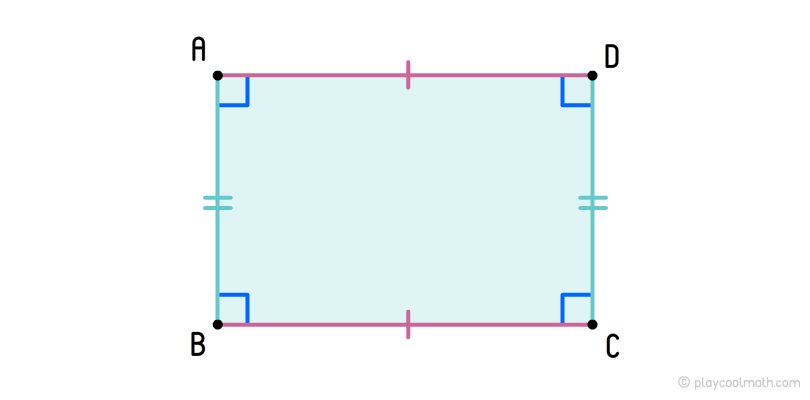
Rectangle
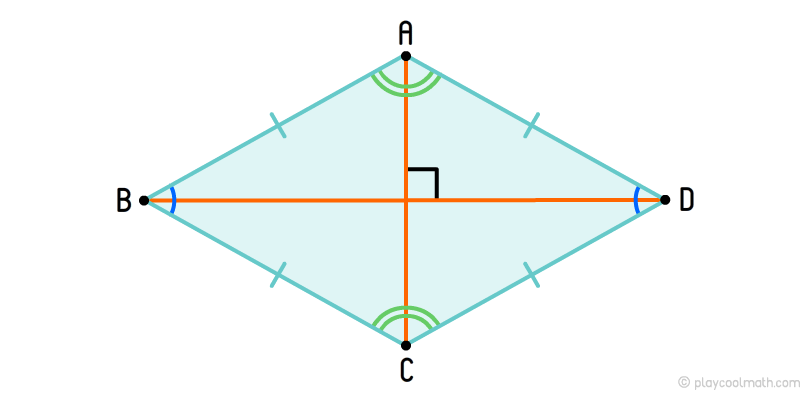
Rhombus
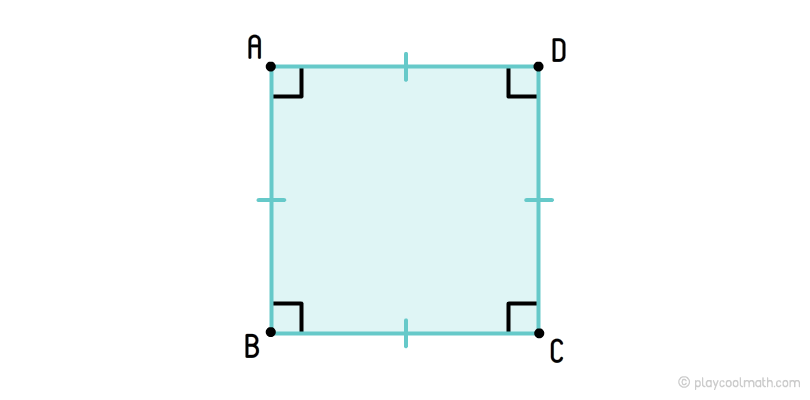
Square
A square is a rectangle with equal sides. A square is a convex quadrangle having all sides and angles equal. All angles of the square should be 90°.
Trapezoid
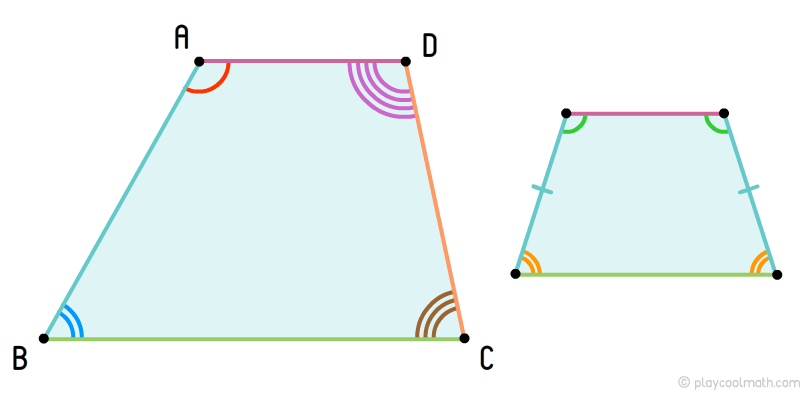
The trapezoid with equal hips is called an isosceles trapezoid. The angles at the bases are equal in an isosceles trapezium. The image to the right represents an isosceles trapezoid.
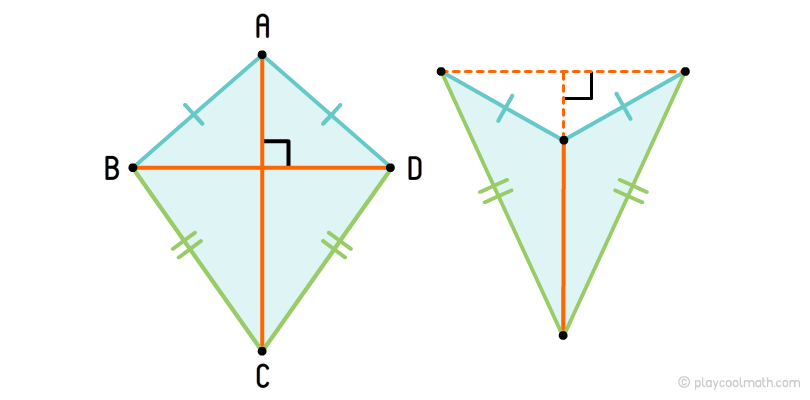
Deltoid
Antiparallelogram
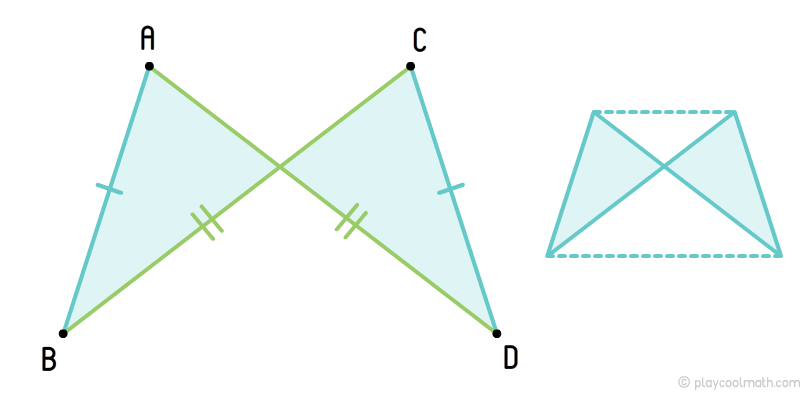
If we draw a convex geometric figure through antiparallelogram vertices, we will get an isosceles trapezoid.
How to write a circle into a quadrangle?
A circle tangent to all four quadrangle sides is called the inscribed circle of a quadrangle. A circle can be inscribed in a quadrangle only under the condition that the sum of the opposite sides is equal. If it is not so, it is impossible to inscribe a circle in a quadrangle.
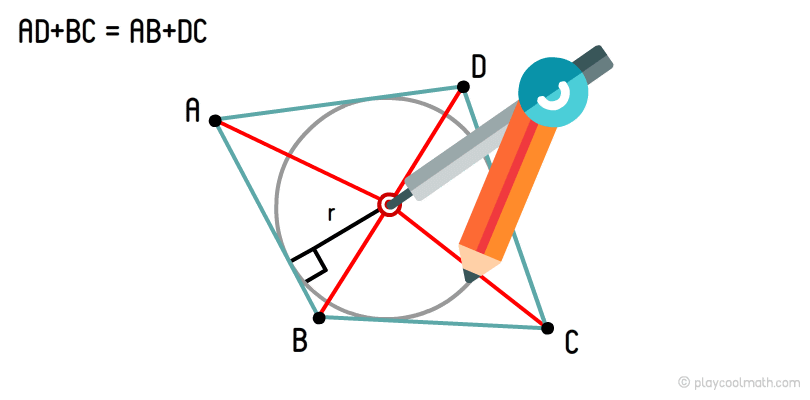
The center of the inscribed circle of a quadrangle is the point of intersection of all the medians of the quadrangle. If we measure the distance along the perpendicular from this point to any base, we will get the radius of the inscribed circle.
How to describe a quadrangle with a circle?
A circle passing through all vertices of a quadrangle is called the circumscribed circle. If the sum of the opposite angles is 180°, this quadrangle might be described by a circle. If it cannot be satisfied, the quadrangle cannot be described by a circle.
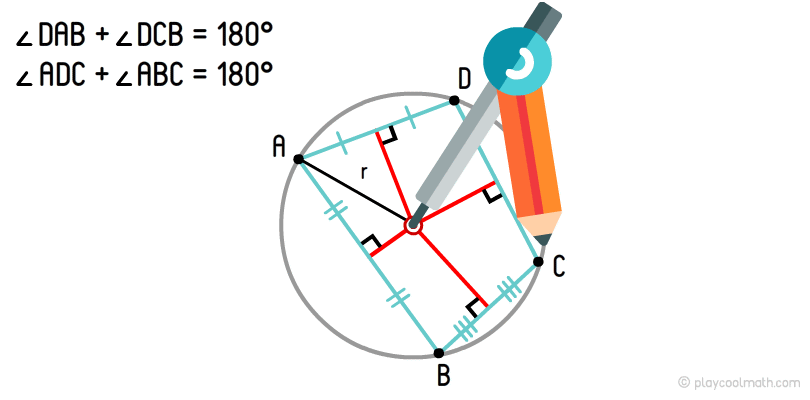
The center of the circumscribed circle of a quadrilateral is the point of intersection of perpendiculars coming from side midpoints.
We have already drawn the circumscribed circle for a triangle. The algorithm to describe the circle for a quadrangle is similar. The image clearly represents how from the middle of the sides we held perpendiculars and found the intersection point. With the help of the caliper, we set the radius from the center to any vertex and draw the circumscribed circle of the quadrangle with a circular motion.
Find orthogonal quadrangles.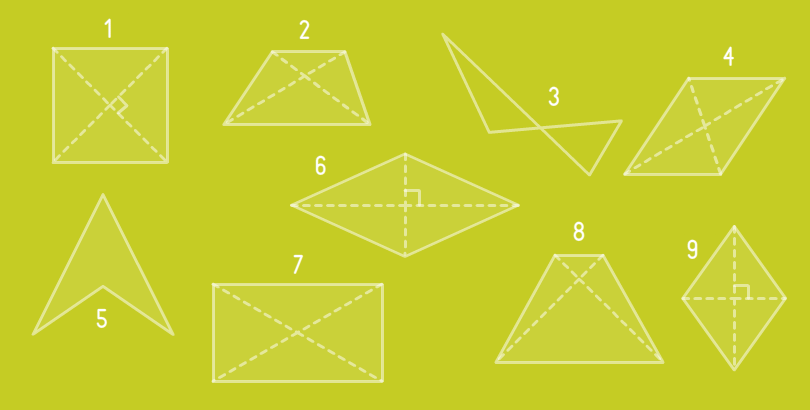
- #1
- #6
- #9