У попередньому уроці ми познайомилися з трикутниками. Дізналися, які трикутники бувають, чим друг від друга відрізняються та які загальні ознаки відповідають для всіх трикутників. У цьому уроці ми дізнаємося, що таке чотирикутник. Почнемо наш урок з визначення чотирикутника.
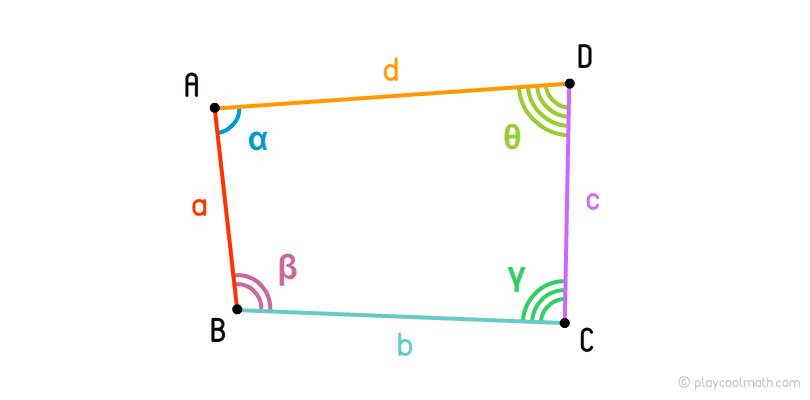
Чотирикутник включає себе такі найпростіші фігури
- Чотири крапки (A, B, C, D);
- Чотири відрізки (AB, BC, CD, DA);
- Чотири кута (α, β, γ, θ);
- Замкнута ламана лінія (ABCD).
Вершини чотирикутника
Вершини чотирикутника позначають великими латинськими літерами. Чотирикутник позначається послідовністю вершин. На малюнку у нас чотирикутник ABCD.
Сторони чотирикутника
Сторони чотирикутника (або ще їх називають межі або ребра) позначаються малими латинськими буквами. На малюнку ми позначили боку чотирикутника буквами a, b, c, d. Також сторони трикутника можна позначати у вигляді відрізків, наприклад a = AB, b = BC, c = CD, d = DA. Сторони, які відносяться до однієї вершині, називаються суміжними сторонами. На малюнку для вершини A ми маємо суміжні сторони DA та AB
Кути чотирикутника
Кути, як ми знаємо, позначають малими грецькими буквами. На малюнку кути чотирикутника позначені як α, β, γ, θ, де α = DAB, β = ABC, γ = BCD, θ = CDA. Кожен кут чотирикутника має протилежний кут, наприклад, на малюнку кут α має протилежний кут γ, а для β протилежні кут θ.
Діагоналі чотирикутника
Всього у чотирикутника дві діагоналі. На малюнку відрізки AC та BD - це діагоналі чотирикутника ABCD.
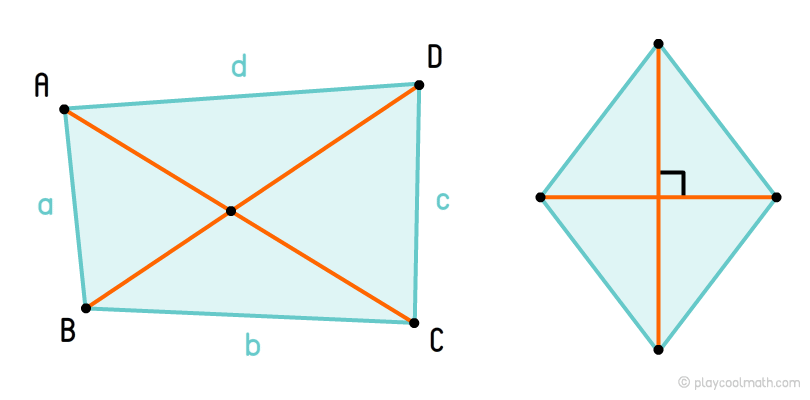
Якщо діагоналі чотирикутника перетинаються під прямим кутом, то такий чотирикутник називається ортодіагональним.
Бісектриси чотирикутника
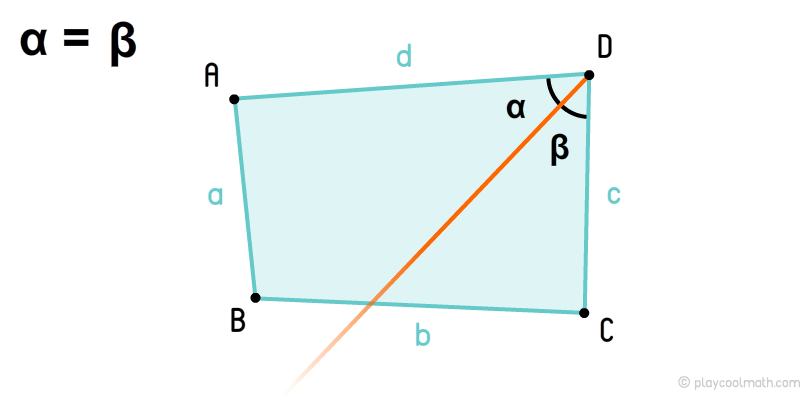
У лекції по трикутниках ми докладно описали, як можна знайти бісектрису для вершини за допомогою транспортира.
Середні лінії чотирикутника
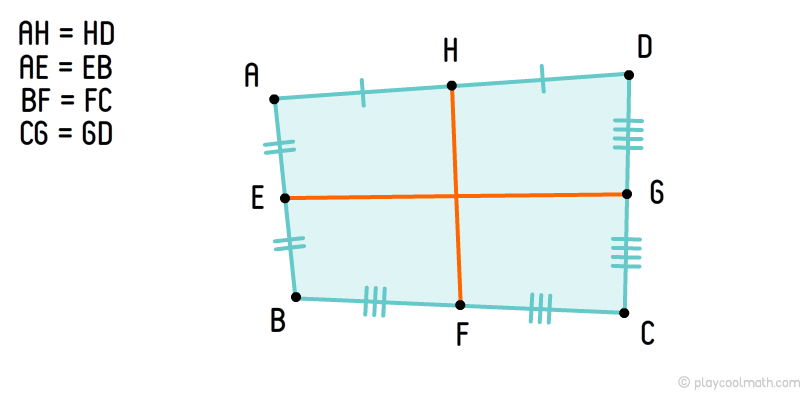
Щоб намалювати середню лінію необхідно всі сторони чотирикутника розбити на два рівних відрізка та знайти середини. Середини протилежних сторін необхідно з'єднати відрізками, які й будуть середніми лініями чотирикутника.
Класифікація трикутників
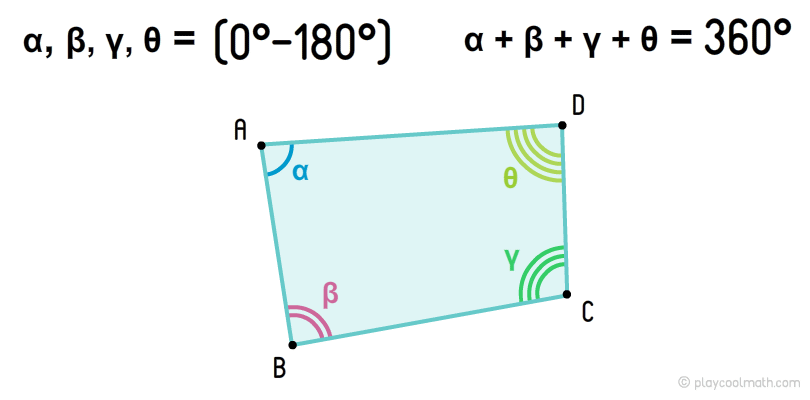
Опуклі чотирикутники
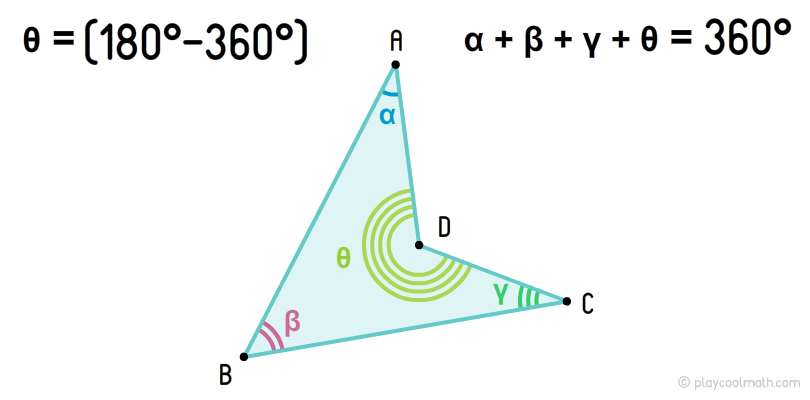
Неопуклі або увігнуті чотирикутники
Самоперетинаючі чотирикутники
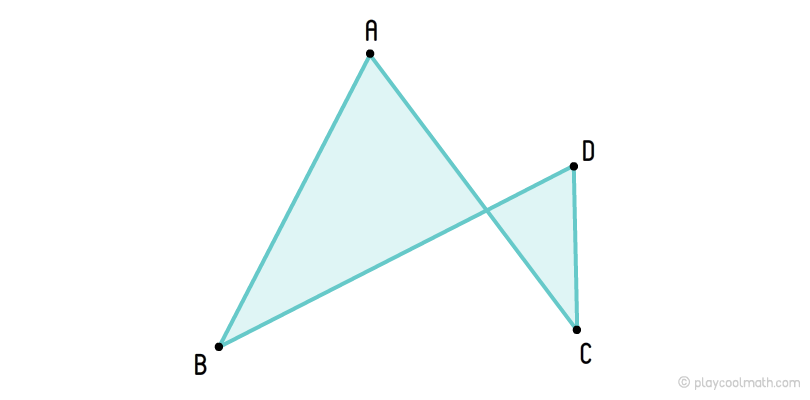
Візуально самопересекающийся чотирикутник схожий на два трикутника у яких сторони лежатимуть на двох пересічних лініях, а крапка перетину це загальна вершина для трикутників.
Види трикутників та їх властивості
Паралелограм
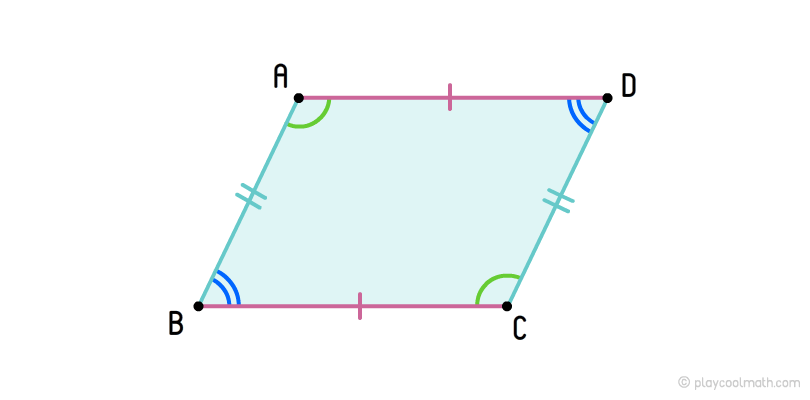
Прямокутник
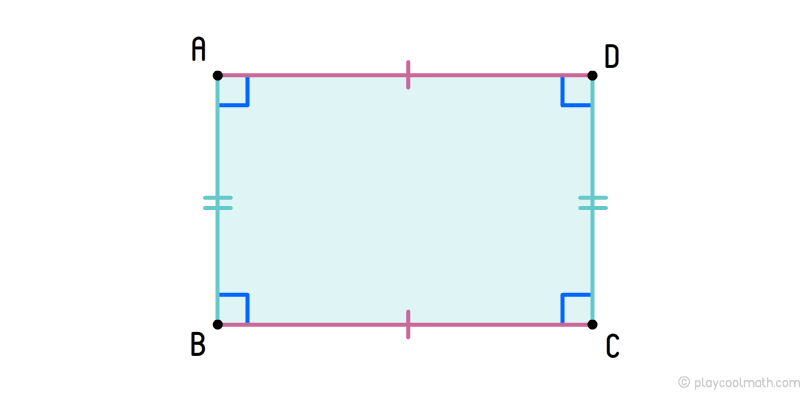
Ромб
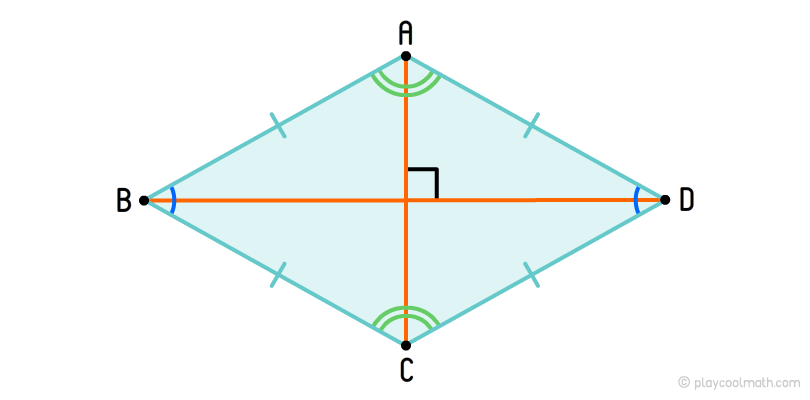
Квадрат
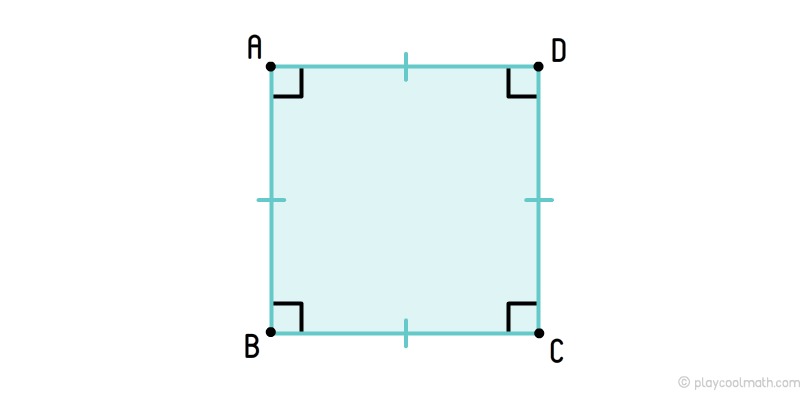
Трапеція
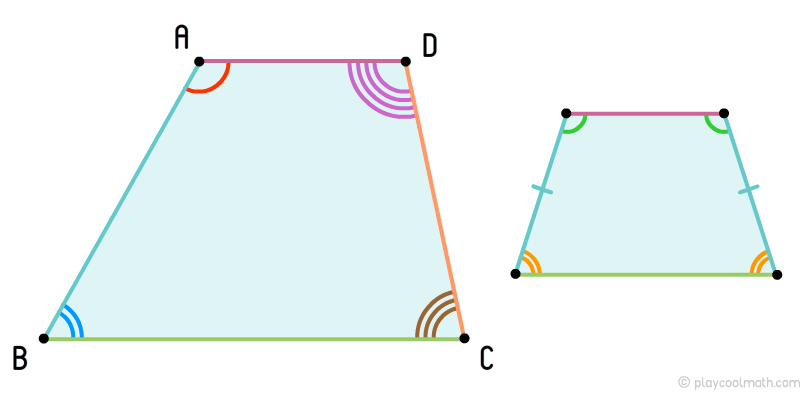
Трапеція, у якої боки рівні, називають рівнобічною трапецією. У рівнобічної трапеції кути у підстав рівні. На малюнку праворуч зображена рівнобічна трапеція.
Дельтоид
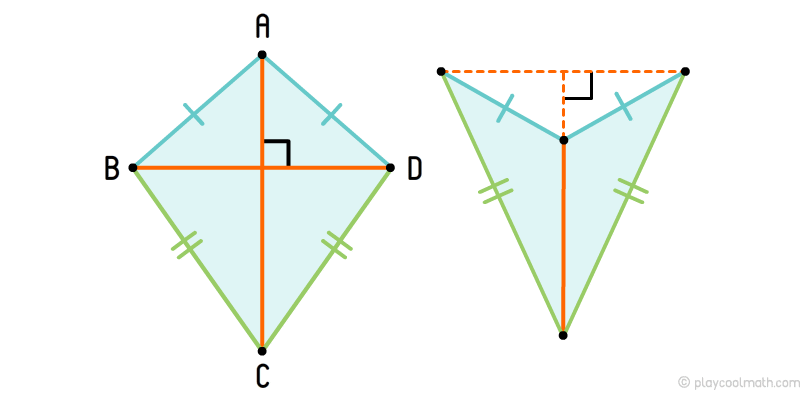
Антипаралелограм
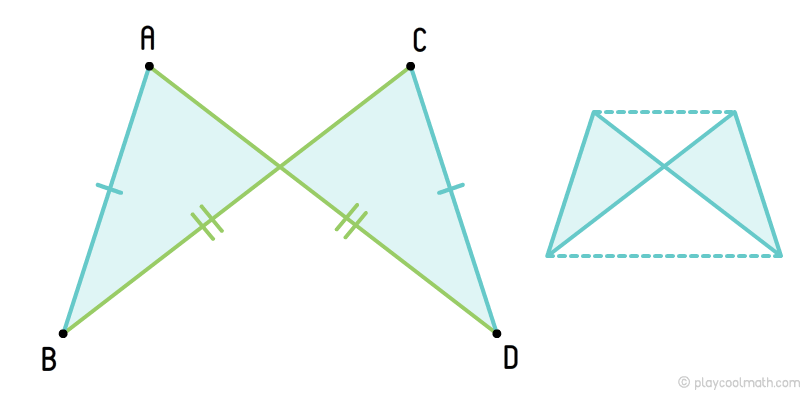
Якщо провести опуклу геометричну фігури через вершини антипаралелограма, то у нас вийде рівнобічна трапеція.
Як вписати окружність в чотирикутник?
Окружність, що дотикается всіх чотирьох сторін чотирикутника, називається вписаною окружністю чотирикутника. У чотирикутник можна вписати коло тільки за однієї умови, що суми протилежних сторін рівні. Якщо умова рівності протилежних сторін не виконується, то в такий чотирикутник неможливо вписати коло.
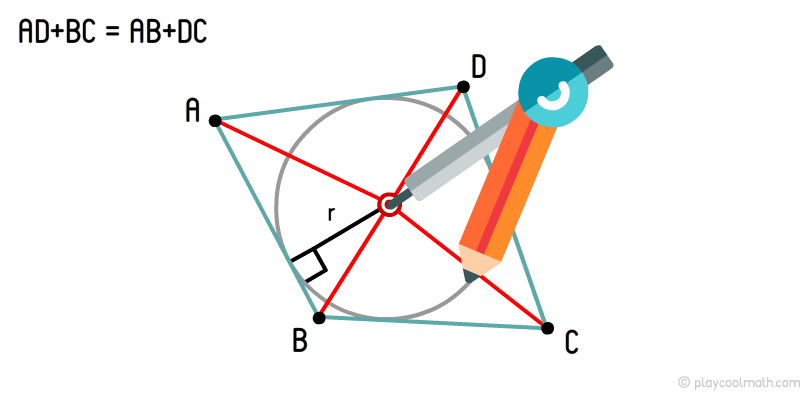
Центр вписаного кола чотирикутника - це точка перетину всіх медіан чотирикутника. Якщо від цієї точки до будь-якого підстави виміряти відстань по перпендикуляру, то ми отримаємо радіус вписаного кола.
Як описати чотирикутник окружністю?
Коло, що проходить по всіх вершинах чотирикутника, зветься описаної окружністю. Якщо сума протилежних кутів дорівнює 180°, то такий чотирикутник можна описати колом. У разі, якщо ця умова не виконується, то такий чотирикутник неможливо описати колом.
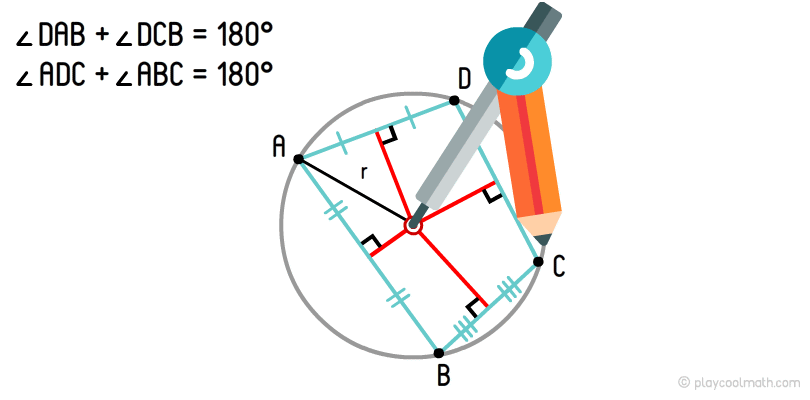
Центр описаного кола чотирикутника - це точка перетину перпендикулярів, що виходять з середини сторін.
Ми вже малювали описану окружність для трикутника. Алгоритм для опису кола для чотирикутника такий же. На малюнку добре видно, як з середини сторін ми провели перпендикуляри і знайшли точку перетину. За допомогою штангенциркуля виставляємо радіус від центру до будь-якої вершини і круговим рухом малюємо описану окружність чотирикутника.
Знайди ортодіагональние чотирикутники. 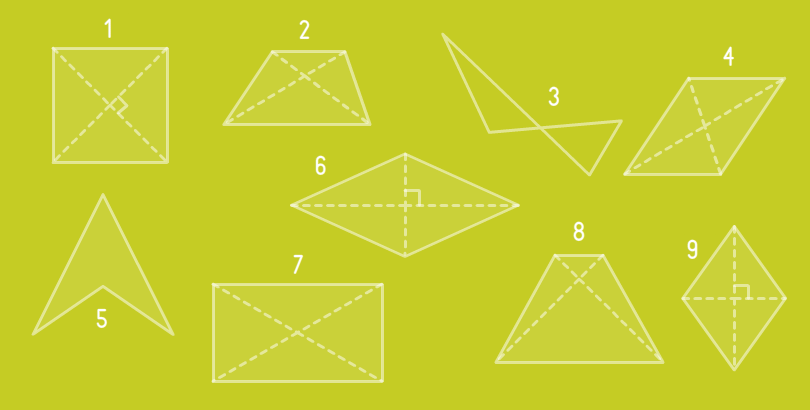
- #1
- #6
- #9