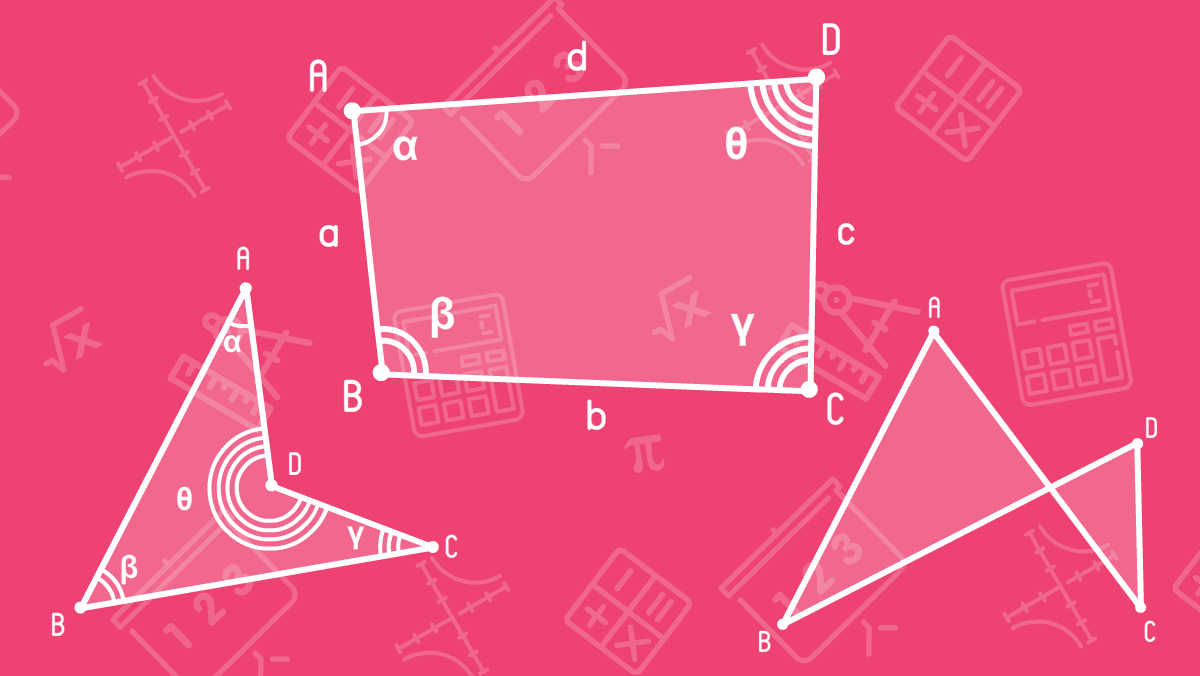
В предыдущем уроке мы познакомились с треугольниками. Узнали, какие треугольники бывают, чем друг от друга отличаются и какие общие признаки соответствуют для всех треугольников. В этом уроке мы узнаем, что такое четырехугольник. Начнем наш урок с определения четырехугольника.
Четырехугольник включает себя такие простейшие фигуры
- Четыре точки (A, B, C, D);
- Четыре отрезка (AB, BC, CD, DA);
- Четыре угла (α, β, γ, θ);
- Замкнутая ломаная линия (ABCD).
Вершины четырехугольника
Вершины четырехугольника обозначают заглавными латинскими буквами. Четырехугольник обозначается последовательностью вершин. На рисунке у нас четырехугольник ABCD.
Стороны четырехугольника
Стороны четырехугольника (или еще их называют грани или ребра) обозначаются строчными латинскими буквами. На рисунке мы обозначили стороны четырехугольника буквами a, b, c, d. Также стороны треугольника можно обозначать в виде отрезков, например a = AB, b = BC, c = CD, d = DA. Стороны, которые относятся к одной вершине, называются смежными сторонами. На рисунке для вершины A мы имеем смежные стороны DA и AB
Углы четырехугольника
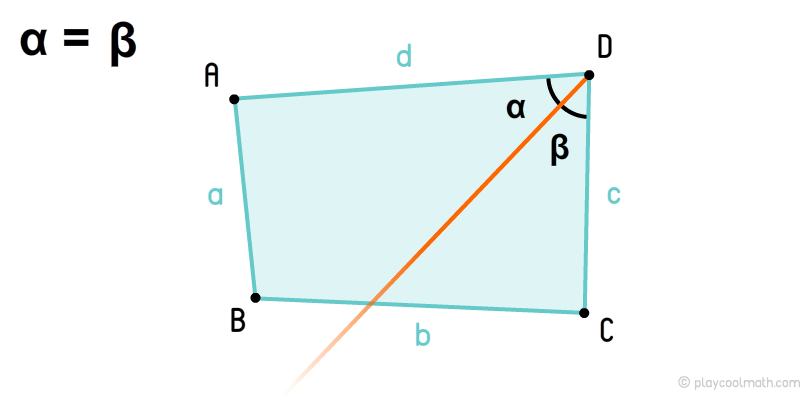
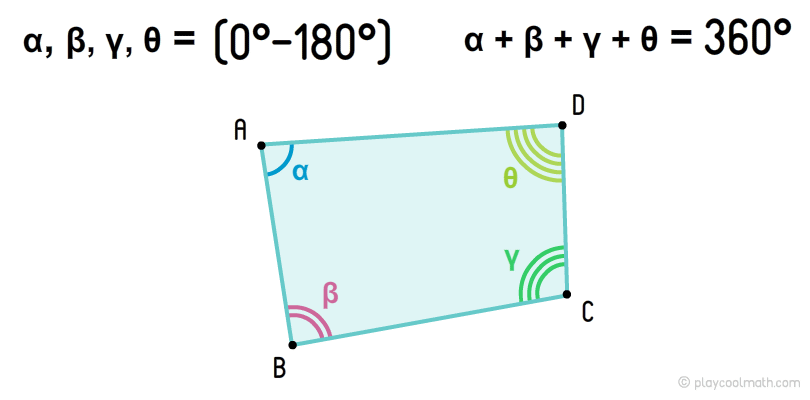
Углы, как мы знаем, обозначают строчными греческими буквами. На рисунке углы четырехугольника обозначены как α, β, γ, θ, где α = DAB, β = ABC, γ = BCD, θ = CDA. Каждый угол четырехугольника имеет противолежащий угол, например, на рисунке угол α имеет противолежащий угол γ, а для β противолежащий угол θ.
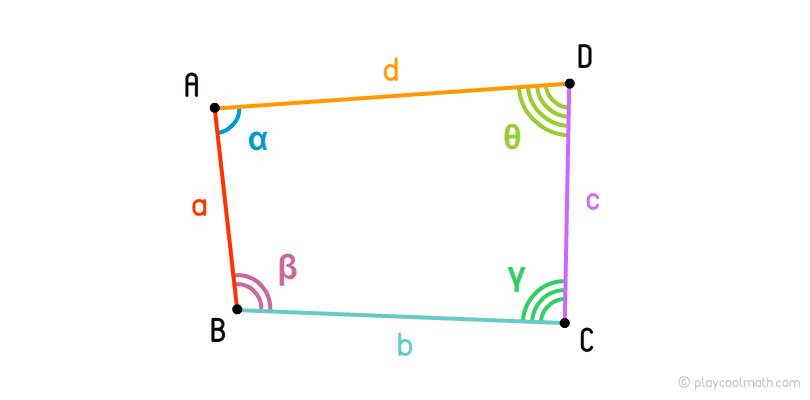
Диагонали четырехугольника
Всего у четырехугольника две диагонали. На рисунке отрезки AC и BD - это диагонали четырехугольника ABCD.
Если диагонали четырехугольника пересекаются под прямым углом, то такой четырехугольник называется ортодиагональным.
Биссектрисы четырехугольника
В лекции по треугольникам мы подробно описали, как можно найти биссектрису для вершины с помощью транспортира.
Средние линии четырехугольника
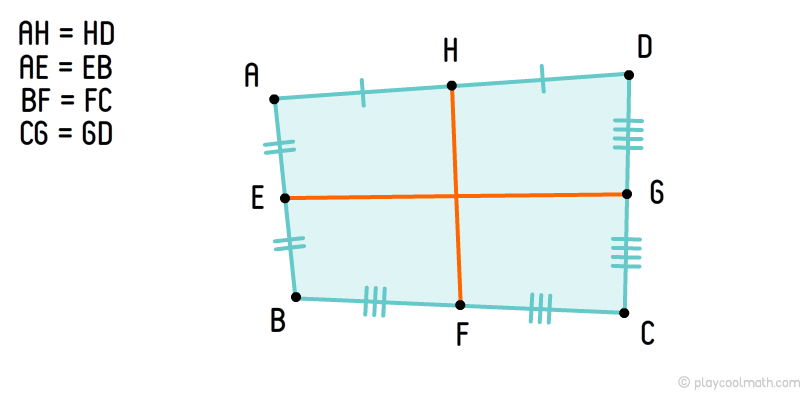
Чтобы нарисовать среднюю линию необходимо все стороны четырехугольника разбить на два равных отрезка и найти середины. Середины противоположных сторон необходимо соединить отрезками, которые и будут средними линиями четырехугольника.
Классификация треугольников
Выпуклые четырехугольники
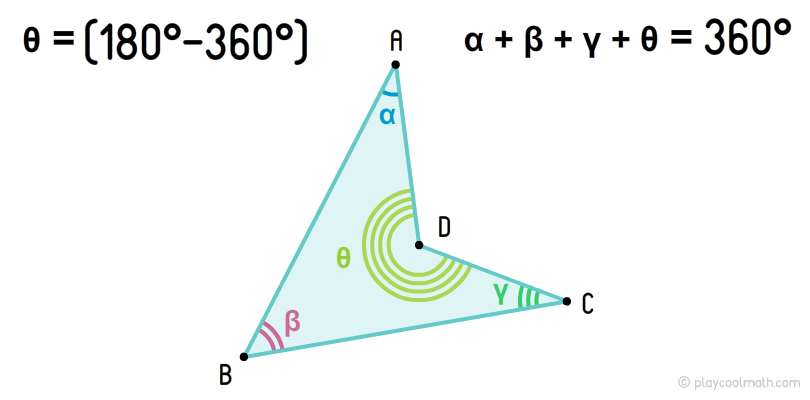
Невыпуклые или вогнутые четырехугольники
Самопересекающиеся четырехугольники
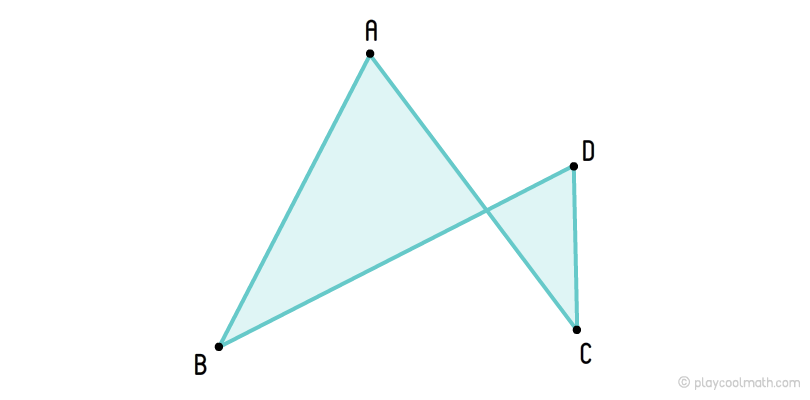
Визуально самопересекающийся четырехугольник похож на два треугольника у которых стороны лежать на двух пересекающихся линиях, а точка пересечения это общая вершина для треугольников.
Виды треугольников и их свойства
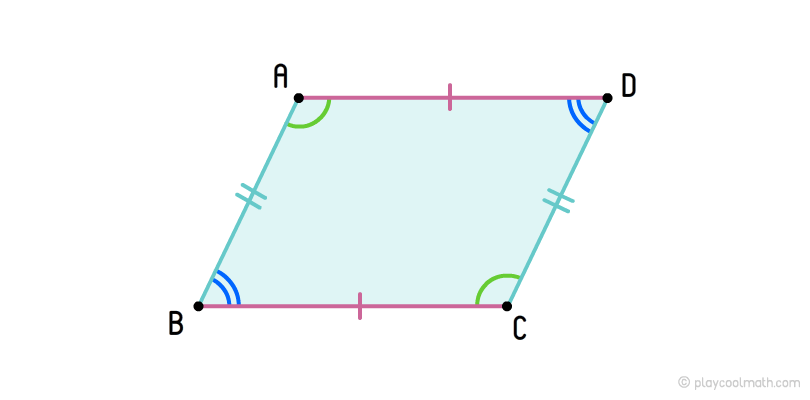
Параллелограмм
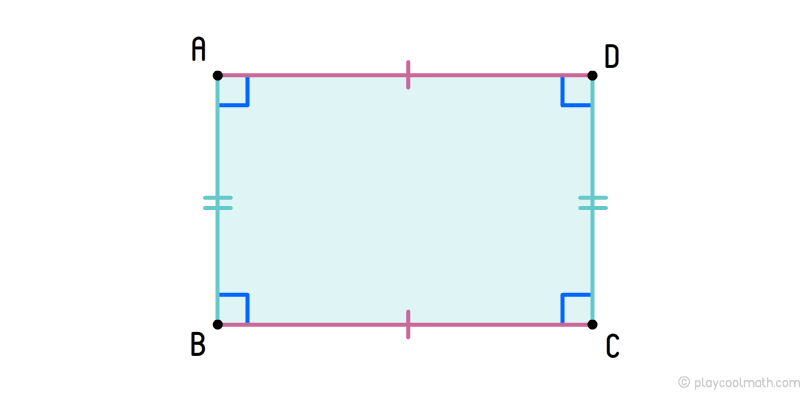
Прямоугольник
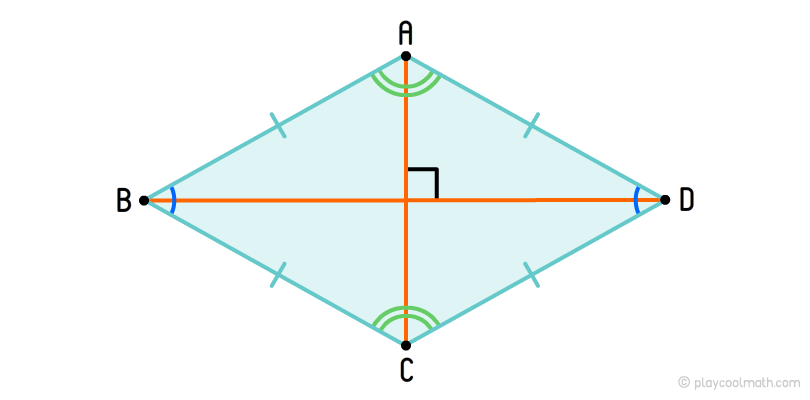
Ромб
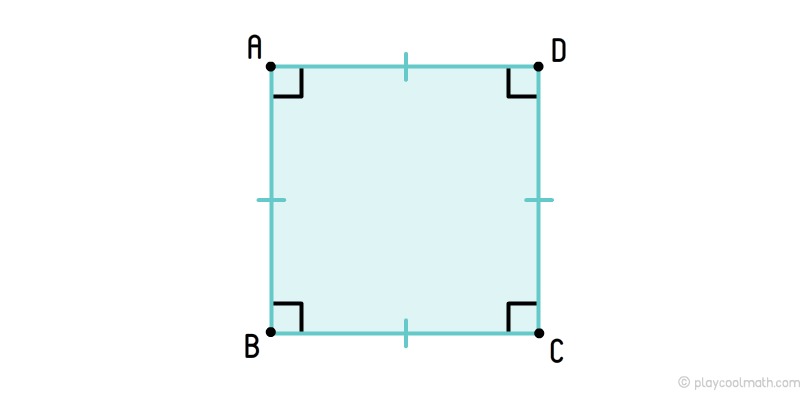
Квадрат
Трапеция
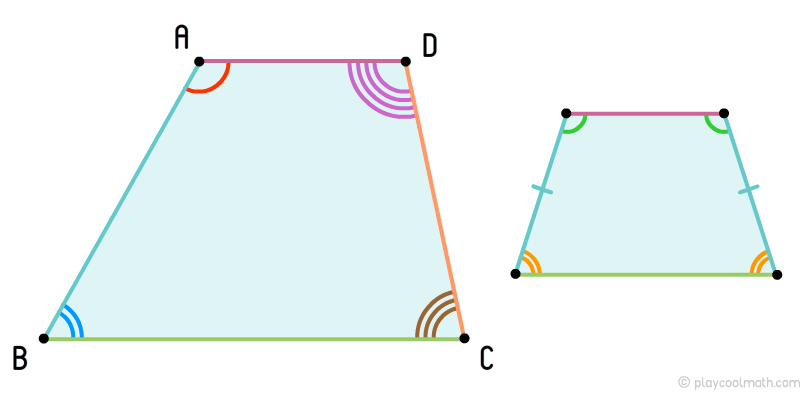
Трапеция, у которой бедра равны, называют равнобедренной трапецией. У равнобедренной трапеции углы у оснований равны. На рисунке справа изображена равнобедренная трапеция.
Дельтоид
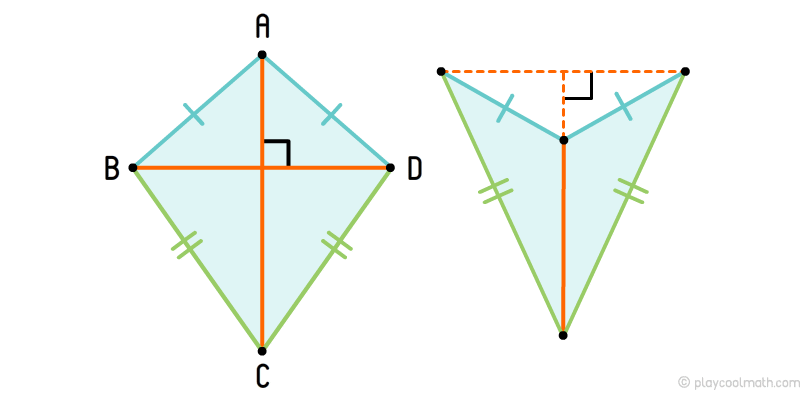
Антипараллелограмм
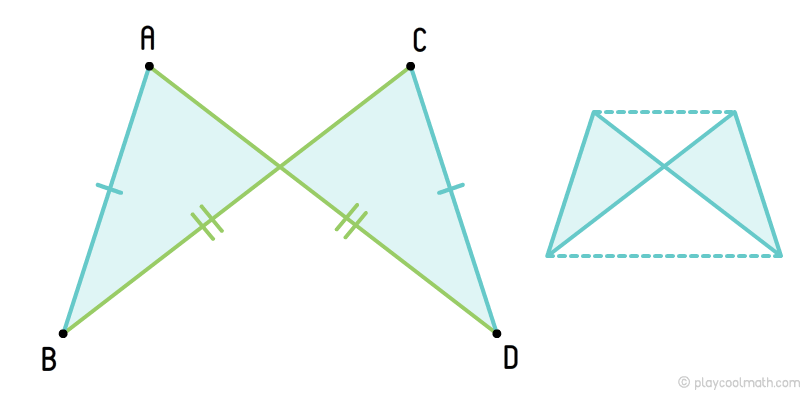
Если провести выпуклую геометрическую фигуры через вершины антипараллелограмма, то у нас получится равнобедренная трапеция.
Как вписать окружность в четырехугольник?
Окружность, касающаяся всех четырех сторон четырехугольника, называется вписанной окружностью четырехугольника. В четырехугольник можно вписать окружность только при одном условии, что суммы противоположных сторон равны. Если условие равенства противоположных сторон не выполняется, то в такой четырехугольник невозможно вписать окружность.
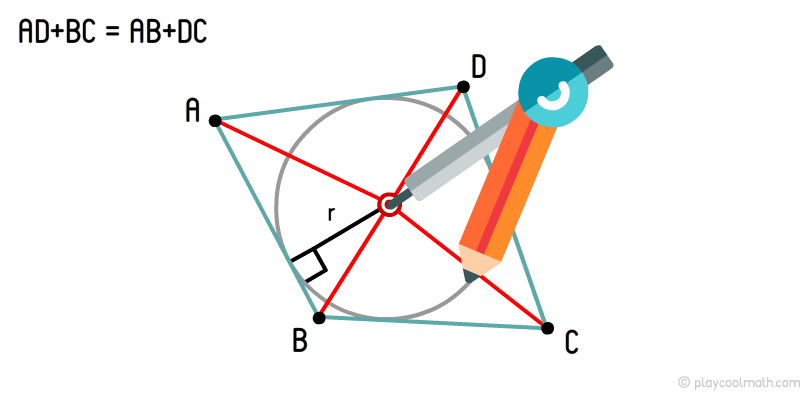 Центр вписанной окружности четырехугольника - это точка пересечения всех медиан четырехугольника. Если от этой точки до любого основания измерить расстояние по перпендикуляру, то мы получим радиус вписанной окружности.
Центр вписанной окружности четырехугольника - это точка пересечения всех медиан четырехугольника. Если от этой точки до любого основания измерить расстояние по перпендикуляру, то мы получим радиус вписанной окружности.
Как описать четырехугольник окружностью?
Окружность, проходящая по всем вершинам четырехугольника, называется описанной окружностью. Если сумма противоположных углов равна 180°, то такой четырехугольник можно описать окружностью. В случае, если данное условие не выполняется, то такой четырехугольник невозможно описать окружностью.
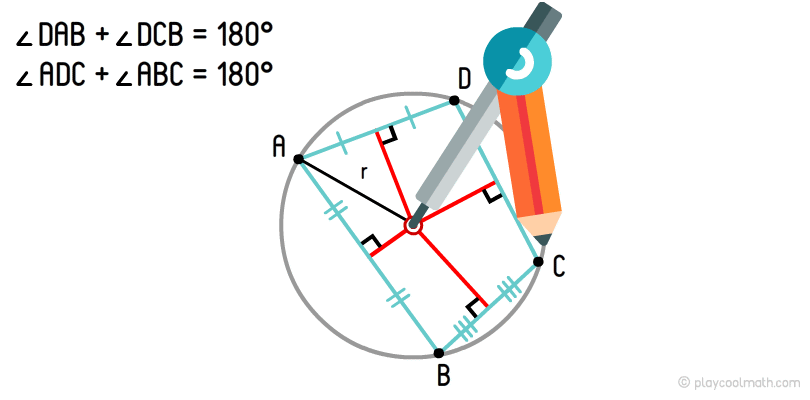 Центр описанной окружности четырехугольника - это точка пересечения перпендикуляров, выходящих из середины сторон.
Центр описанной окружности четырехугольника - это точка пересечения перпендикуляров, выходящих из середины сторон.
Мы уже рисовали описанную окружность для треугольника. Алгоритм для описания окружности для четырехугольника такой же. На рисунке хорошо видно, как из середины сторон мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность четырехугольника.
Найди ортодиагональные четырехугольники. 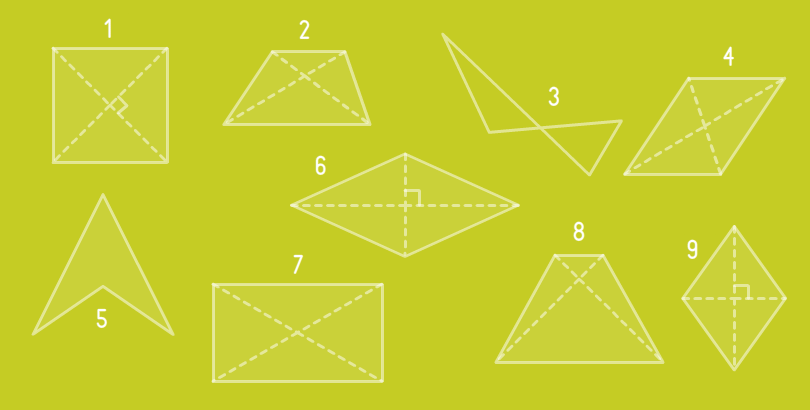
- #1
- #6
- #9