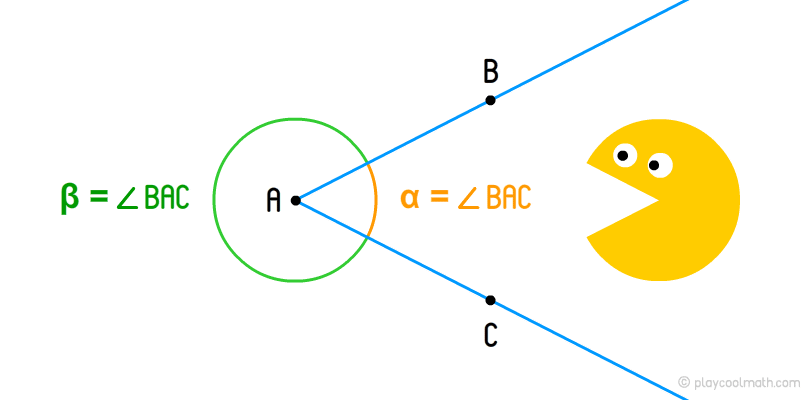
An angle is a geometric shape formed by two rays. Their initial point is the same. This point is called the angle vertex, the rays are called the angle sides. The angle sides divide the plane into 2 regions, they are called flat angles or simply angles. The smaller angle is called the inner angle, and the larger one is called the outer angle.
Angles can also be designated as three points. Let’s say, ABC. In this record, B is a vertex, and A and C are points lying on different rays of the angle. To simplify and record fast, angles are usually defined by lowercase Greek letters: α - alpha, β - beta, γ - gamma, θ - theta, φ - fi, etc. The angle is denoted by a two-line symbol meaning the angle.
On the picture, you see two rays AB and AC with a vertex at point A forming two angles: α - internal angle, β - external angle.
Angular measure
The angular measure allows comparing the angles between each other. It means that knowing the angle measure we can say that this angle is either greater than the other one, or smaller, or they are equal. There are several measures of angles:
- in degrees, minutes, seconds;
- in radians;
- in turns;
In maths, the first type of the angle measure is more widespread - degrees, minutes, seconds. Let’s learn it in details. Look at the clock shown below.
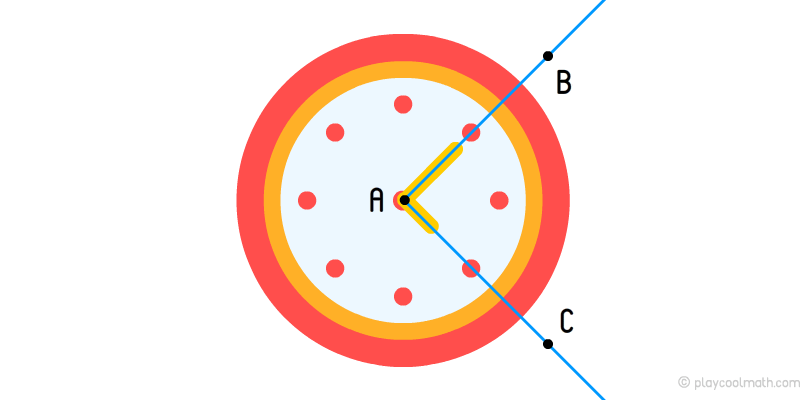
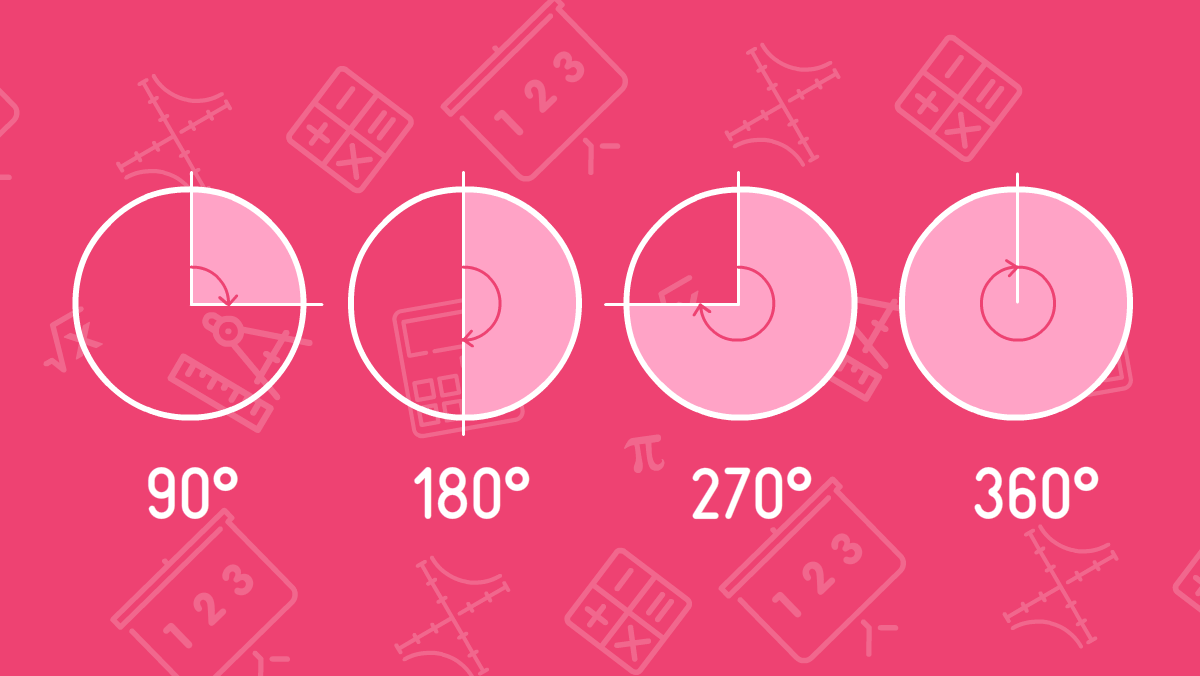
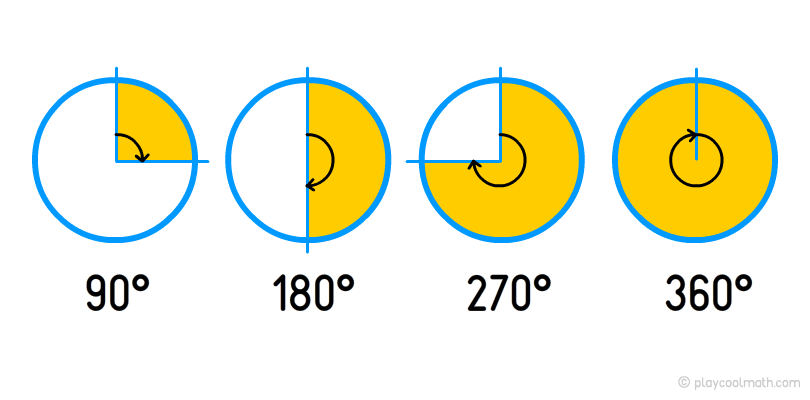
If you look at the clock, you see the hands of the clock as rays where the starting point is the same as the center of the dial. The complete rotation of the arrow makes 360 degrees. The degree is defined by the symbol °. If the needle makes a half of the turn, it moves 180 degrees or 180°. If it makes a quarter, it moves 90°. In the picture below, you can see what time corresponds to each angle when the time varies. It means that 15:00 corresponds to an angle of 90°, 18:00 corresponds to an angle of 180°, 21:00 to 270° and 24:00 to 360 °. The sum of the outer and inner angles should always be 360°.
You will study the angular measure in details in other maths sections: geometry and trigonometry.
Types of Angles
Depending on the angle measure the types of angles are as follows:
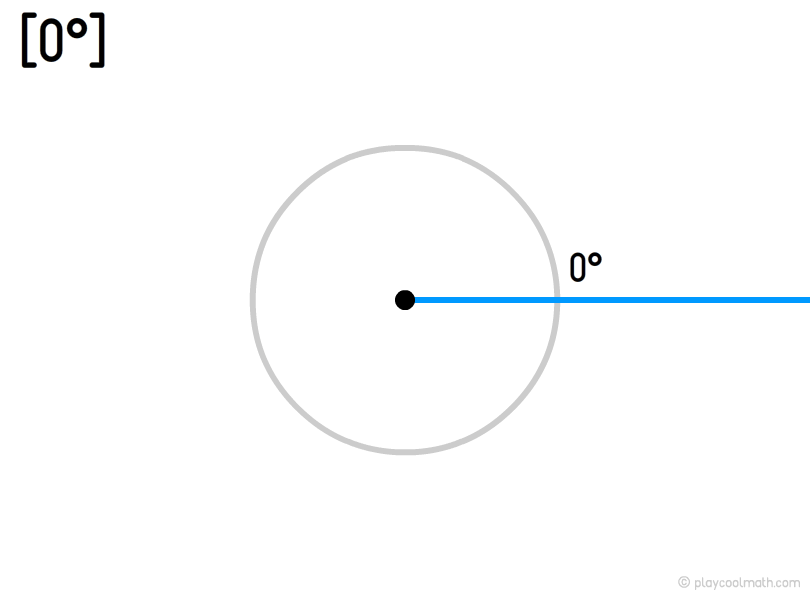
Zero angle
A zero angle is an angle where two sides coincide. Two equally directed rays emerge from the vertex. The zero angle is 0°.
Acute angle
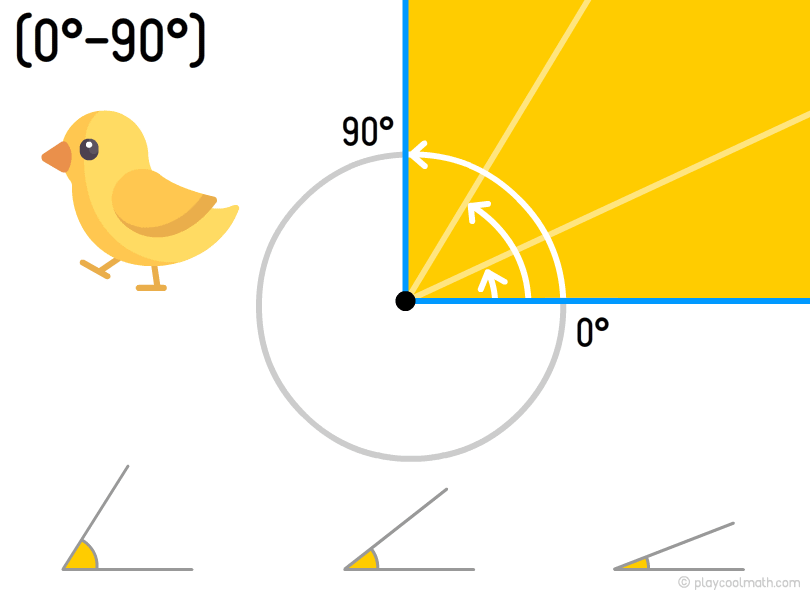
An acute angle is lying from 0 ° to 90 ° where 0 and 90 do not enter into this frame.
An acute angle is easy to remember. All sharp objects have an acute angle like a beak of a bird, an awl, a kitchen knife. You can see a yellow border on the picture showing the maximum measure of the right angle.
Right angle
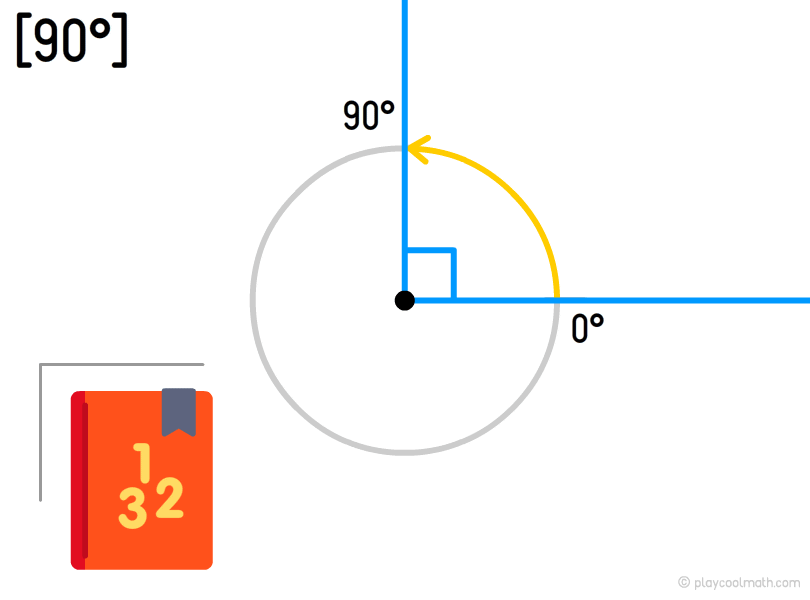
A right angle is the angle with perpendicular sides equal to 90°.
A right angle is a small square at the bottom of the angle as shown below.
Obtuse angle
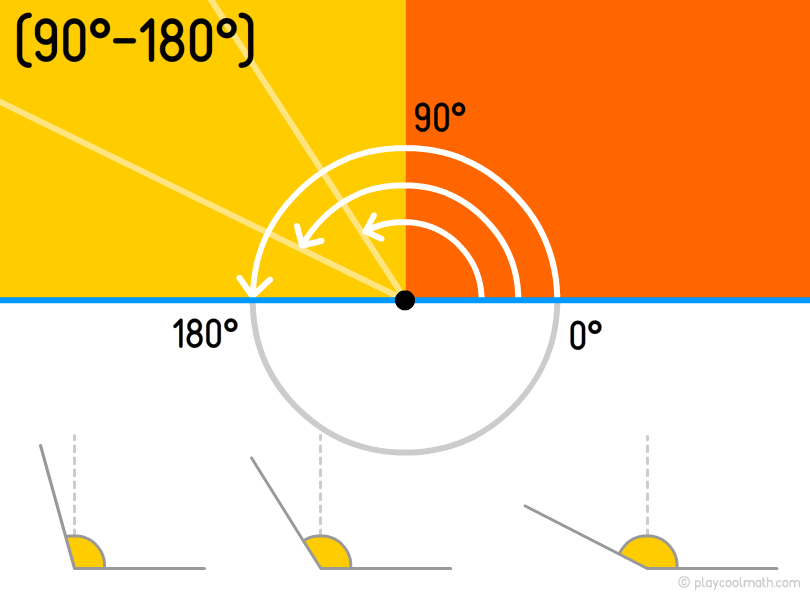
An obtuse angle is lying between 90° and 180° where 90° and 180° are not included.
Oblique angle
An oblique angle means an angle different from 0°, 90°, 180° or 270°.
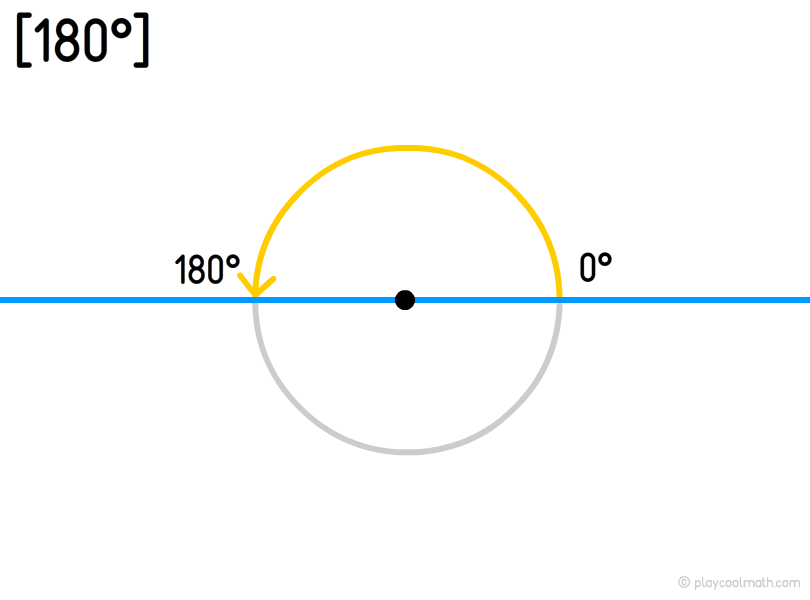
Straight angle
A straight angle equals to 180°, its rays go to opposite directions.
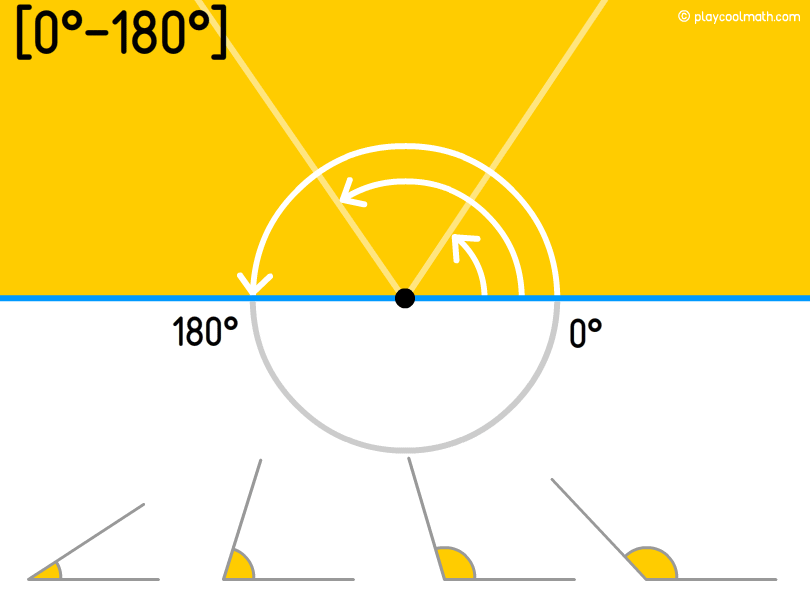
Convex angle
A convex angle is an angle between 0 ° to 180 ° the boarding values included.
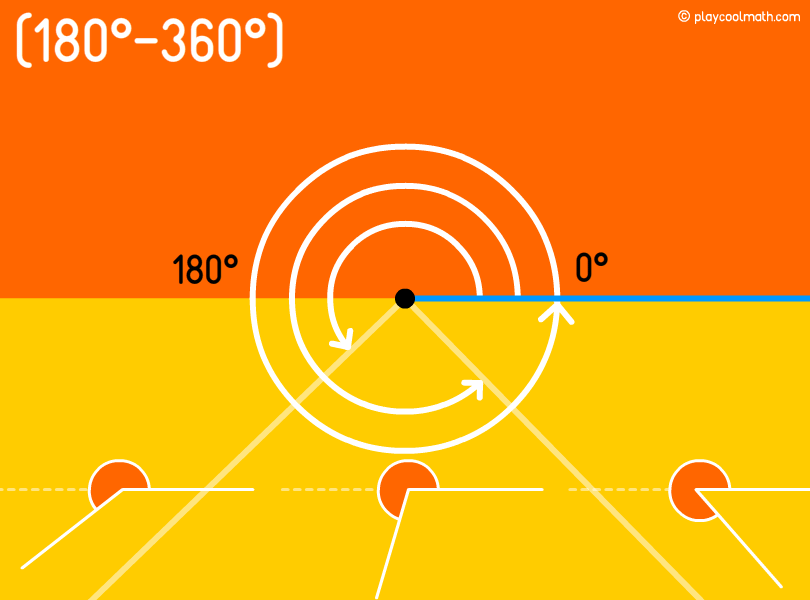
Non-convex, or concave angle
A non-convex angle or a concave angle is an angle lying within 180 ° and 360 ° where boundary values are not included.
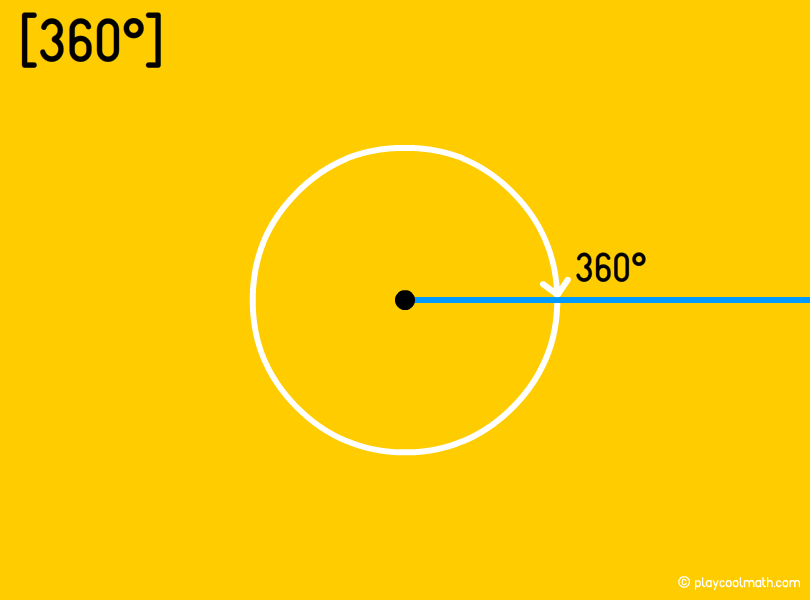
Full angle
A full angle is the one with two coinciding sides. It is the opposite of a zero angle. The full angle equals to 360°.
A zero and a full angles have the same sides. A zero angle is an internal angle of 0°, and a full angle is an outer angle equal to 360°.
Look at the picture and count the number of angles of each type?
- Zero angle - 2;
- Acute angle - 3;
- Right angle - 2;
- Obtuse angle - 2;
- Oblique angle - 6;
- Straight angle - 1;
- Convex angle - 10;
- Concave angle - 1;
- Full angle - 1;