The simplest geometric shapes are shapes that make more complex geometric shapes. We need bricks to build a house. We need the simplest shapes to create complex shapes. The simplest geometric shapes are as follows: a point, a line, a ray, a segment and a broken line.
Note that we study geometric shapes on a plane. A plane means an endless surface. Just imagine, there is a piece of paper on the table. A plane is an endless piece of paper where we will draw various geometric shapes. We are going to study and to draw.
Point
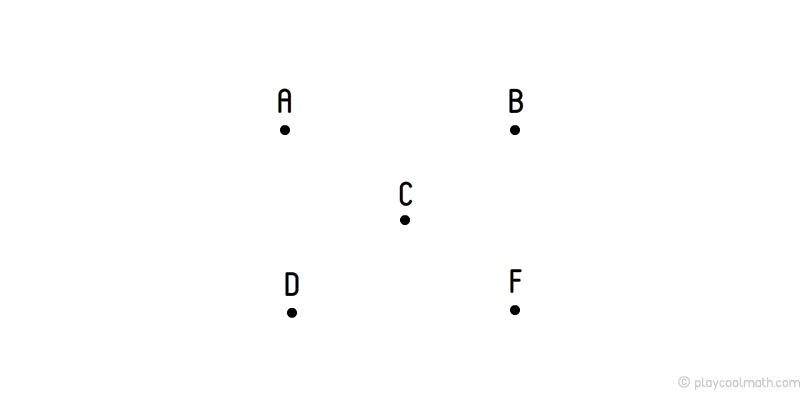
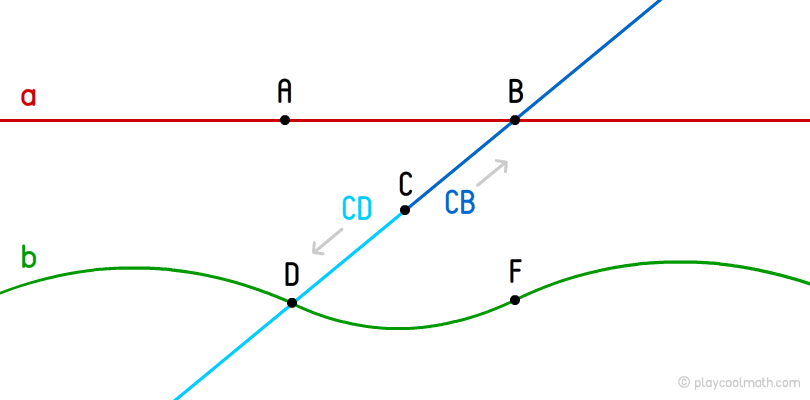
A point is the simplest figure. A point is a very important figure because it can be used to create all the figures. On this picture, we drew the points. We can draw the points easily. Take a clean piece of paper and touch it slightly with a pencil. Draw some points as it is done in the picture below. The points are defined by uppercase Latin letters. In your picture, mark the points with capital letters, for example A, B, C, D, F.
Line
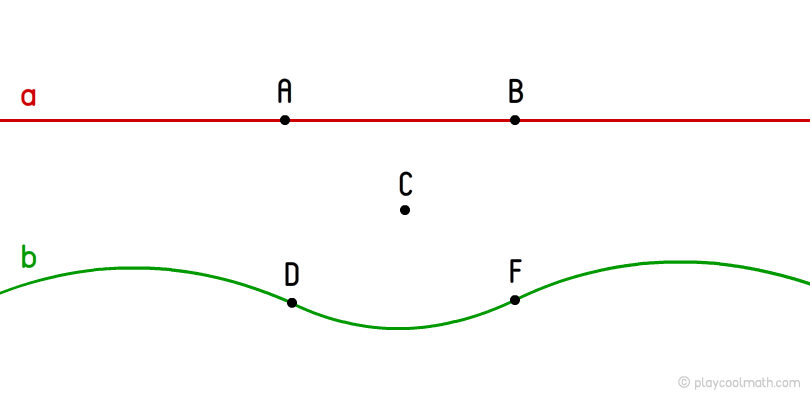
A line as a point is one of basic maths concepts. There are straight and curved lines. A straight line has no start and no ending - it is infinite. It is impossible to show the whole straight line and to measure it. The curved line differs from the straight one as it is curved in shape. It is called the boundary of more complicated geometric shapes. Let's connect points A and B with a straight red line in the picture where you drew the points. The curved line will be marked green connecting points D and F. The lines are defined by small Latin letters. We will put Latin letters a and b in the picture.
Ray or half-line
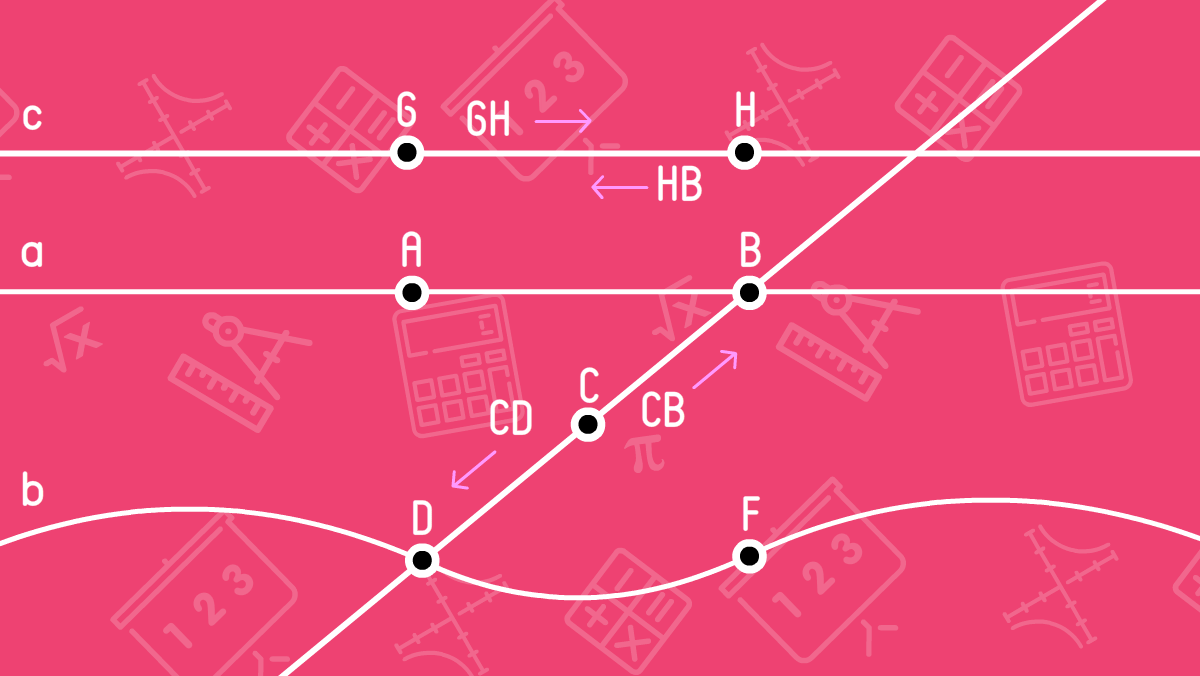
A ray is a part of a line that has a start but has no ending. A ray is goes from a point to infinity. A ray can also be called a half-line. At the beginning of the ray we find the point - the ray start or the starting point of the half-line. Let's draw a blue ray connecting point C and D and passing through point B, and a light blue ray connecting points C and D. The ray is defined by two large Latin symbols where the first symbol is the starting point and the second one is an arbitrary point on the line. The ray has a direction. If we draw a point on a straight line, we will get two rays going to opposite directions. In the picture, we drew 2 rays CB and CD and showed the direction with small arrows.
Segment
A segment is a part of a straight line bounded by two points. These points are the ends of the segment. The points between the ends of the segment on the line are called internal points. We can measure the segment as it is bounded by two points. A segment with ending points G and H is defined as GH or HG. The segment has a direction like a ray. For example, in the picture, the segments GH and HG are the same with different directions. GH goes to the right when HG goes to the opposite direction, to the left.
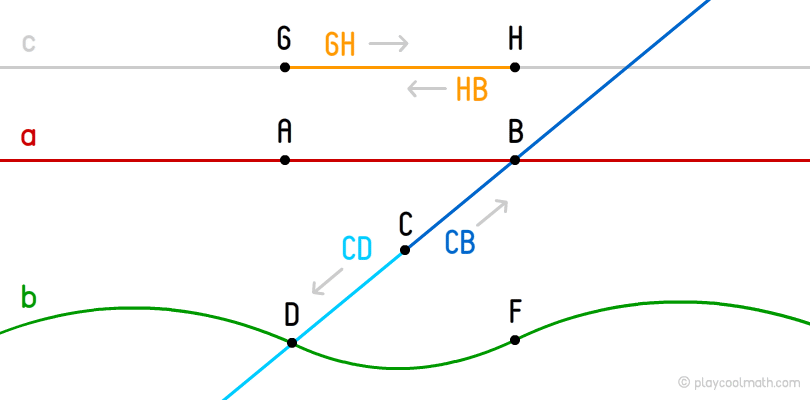
In the picture, find all the segments except GH and HG
- AB and BA;
- DB and BD;
- DC and CD;
- CB and BC.
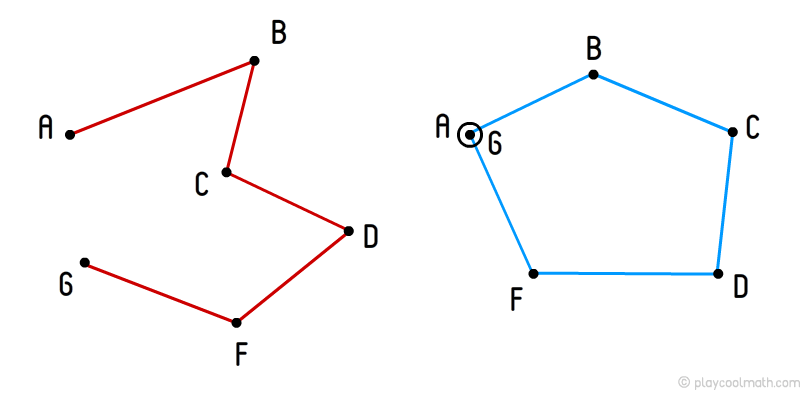
Broken line
A broken line is a group of segments connected accordingly with points of neighboring segments not on one line. The ending point of the segment is the starting point of the new segment. All points in a broken line are called vertices. If the starting point of the first segment coincides with the ending point of the last segment, this broken line is called closed broken line. The broken line is defined by uppercase Latin letters: a list of all vertices in the polyline in order, for example, ABCDFG. In the picture, we drew two broken lines in red and blue. The blue broken line is closed since the first and last vertices coincide.