
In the previous lesson, we found out what numbers and figures mean. In this lesson we’ll learn to break the number into tens, hundreds and thousands, we’ll also learn what number is the largest one.
Hundreds and thousands
If you trained and passed all the tests connected with numbers and figures, you can count up to ten with ease. Let’s look at 100 one more time, it is made of three figures: 1,0 and 0. The location of a figure in the number is called a degree. As we are working in the decimal counting system, the schematic table of degrees can look as follows:
- 0 degree - ones (units);
- 1 degree - tens;
- 2 degree - hundreds;
- 3 degree - thousands.
| Degree | 3 | 2 | 1 | 0 |
| Value | 1000 | 100 | 10 | 1 |
It seems difficult at first glance but it is very simple. Look at the table again. A zero degree defines how many ones a number has. The first degree defines how many tens it has. The second degree defines how many hundreds it has and the third degree defines how many thousands it has. For example, let’s take number 24 and split it into degrees. We know that 24 is made of two figures 2 and 4, so let’s put these figures into a table:
| Degree | 3 | 2 | 1 | 0 |
| Value | 1000 | 100 | 10 | 1 |
| Число 24 | 2 | 4 |
According to this table, it becomes clear that a zero degree has figure 4 and the first degree has figure 2. Pay attention at the values in each column. We have 2 tens and 4 ones - twenty-four.
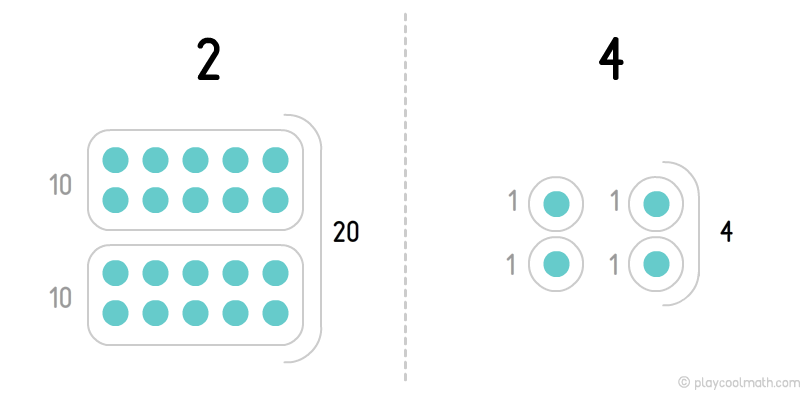
If we count all the points on the image, we’ll get 24, so all the points can be replaced by 24. It is very simple. Let’s make it more complicated and split number 136:
| Degree | 3 | 2 | 1 | 0 |
| Value | 1000 | 100 | 10 | 1 |
| Number 136 | 1 | 3 | 6 |
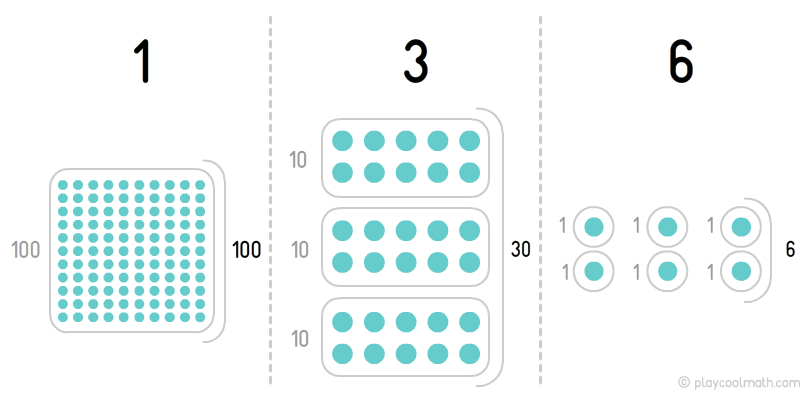
This picture with numerous points can be replaced by one number 136. Like in the previous example, we included number 136 into the table of degrees. We found out that it has 1hundred, 3 tens and 6 ones - one hundred and thirty-six.
And now even more difficult. Let’s split into the degrees the year when America was discovered - 1492:
| Degree | 3 | 2 | 1 | 0 |
| Value | 1000 | 100 | 10 | 1 |
| Number 1492 | 1 | 4 | 9 | 2 |
So, it is 1 thousand, 4 hundreds, 9 tens and 2 ones - one thousand four hundred and ninety-two.
To train yourself, try to pronounce the following numbers: 2468, 4537, 5679, 9999
- 2468 - two thousand four hundred and sixty-eight;
- 4537 - four thousand five hundred and thirty-seven;
- 5679 - five thousand six hundred seventy nine;
- 9999 - nine thousand nine hundred and ninety-nine.
The greatest number
According to the decimal counting system, we learn how to count up to 9999. In order to count further, we need to know the degrees of the number that are multiple to three. In the table below, we’ll describe the degrees for large numbers:
- 0one100 = 1
- 3thousand103 = 1 000
- 6million106 = 1 000 000
- 9milliard or billion109 = 1 000 000 000
- 12trillion1012 = 1 000 000 000 000
- 15quadrillion1015 = 1 000 000 000 000 000
- 18quintillion1018 = 1 000 000 000 000 000 000
- 21sextillion1021 = 1 000 000 000 000 000 000 000
- 24septillion1024 = 1 000 000 000 000 000 000 000 000
- 27octillion1027 = 1 000 000 000 000 000 000 000 000 000
- 30nonillion1030 = 1 000 000 000 000 000 000 000 000 000 000
- 33decillion1033
- 36undecillion1036
- 39duodecillion1039
- 42tredicillion1042
- 45quattuordecillion1045
- 48quindecillion1048
- 51sexdecillion1051
- 54septendecillion1054
- 57octodecillion1057
- 60novemdecillion1060
- 63vigintillion1063
- 66unvigintillion1066
- 69duovigintillion1069
- 72trevigintillion1072
- 75quattuorvigintillion1075
- 78quinvigintillion1078
- 81sexvigintillion1081
- 84septenvigintillion1084
- 87octovigintillion1087
- 90novemvigintillion1090
- 93trigintillion1093
- 96untrigintillion1096
- 99duotrigintillion1099
- 102tretrigintillion10102
We came to degree 30 only, however, decillion can’t fit into the screen. And can you imagine a number with 100 zeros? If you count from 1 to one million loudly and without pause, you will need more than one month. If you count from a million to a milliard you’ll need 3000 years.
In order to show the difference between large numbers, we’ll show the difference between a million and a trillion.

Interesting fact: Googol (googol) — is a number, in the decimal counting system represented by one with 100 zeros:
10100 = 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
In 1938, the famous American mathematician Edward Kasner was walking with his nephew in the park discussing large numbers. A nine-year-old Milton Sirotta suggested a name for a number with 100 zeros - «googol». Later, in 1998, this number gave its name to the most popular search engine.
As you can see, there are no limits to counting. If a number is considered really big, there will always be a larger number. This leapfrog can last endlessly. It is very interesting. You can name any decimal degree if it has no name yet.
We decided to invent a name for a degree 777 in the honor of our website. Let it be playcoolmathgintillion - 10777 . What name would you invent?


